
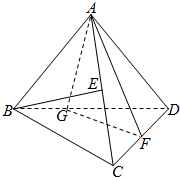
 如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.
如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.分析 (Ⅰ)取CF的中点为H,连EH,BH,EH∥AF,可得∠BEH(或其补角) 即为BE与AF所成角,由已知求解直角三角形可得BH、EH、BE的值,利用余弦定理求得答案;
(Ⅱ)取BD的中点为O,连AO,CO,则$AO=CO=2\sqrt{2}$,利用线面垂直的判定得AO⊥平面BCD.可得$V_{A-BCD}^{\;}=\frac{1}{3}×\frac{1}{2}×4×4×2\sqrt{2}=\frac{{16\sqrt{2}}}{3}$.连DE交AF于M,则M为△ACD的重心,得到${V_{A-FDG}}=\frac{1}{3}{V_{A-BCD}}$,进一步由${V_{A-BCFG}}=\frac{2}{3}{V_{A-BCD}}$得答案.
解答 解:(Ⅰ)取CF的中点为H,连EH,BH,EH∥AF,
∴∠BEH(或其补角) 即为BE与AF所成角.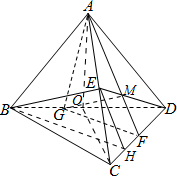
由已知得AB⊥AD,BC⊥CD,CH=1,
∴$BH=\sqrt{17}$,$EH=\sqrt{3},BE=2\sqrt{3}$,
∴$cos∠BEH=\frac{B{E}^{2}+E{H}^{2}-B{H}^{2}}{2BE•EH}=\frac{(2\sqrt{3})^{2}+(\sqrt{3})^{2}-(\sqrt{17})^{2}}{2×2\sqrt{3}×\sqrt{3}}$=$-\frac{1}{6}$.
∴直线BE和AF所成角的余弦值为$\frac{1}{6}$;
(Ⅱ)取BD的中点为O,连AO,CO,则$AO=CO=2\sqrt{2}$,
∴AO⊥OC,AO⊥BD,从而AO⊥平面BCD.
∴$V_{A-BCD}^{\;}=\frac{1}{3}×\frac{1}{2}×4×4×2\sqrt{2}=\frac{{16\sqrt{2}}}{3}$.
连DE交AF于M,则M为△ACD的重心,且$\frac{DM}{ME}=\frac{2}{1}$,
∵BE∥平面AGF,∴BE∥GM,$\frac{DG}{GB}=\frac{2}{1}$.
∴${V_{A-FDG}}=\frac{1}{3}{V_{A-BCD}}$,${V_{A-BCFG}}=\frac{2}{3}{V_{A-BCD}}$=$\frac{{32\sqrt{2}}}{9}$.
点评 本题考查异面直线及其所成的角,考查空间想象能力和思维能力,训练了利用等积法求三棱锥的体积,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国古代数学名著《九章算术》中的更相减损法的思路与图相似.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
我国古代数学名著《九章算术》中的更相减损法的思路与图相似.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,N为线段AC上靠近A点的四等分点,若$\overrightarrow{AP}$=(m+$\frac{1}{10}$)$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{BC}$,则m=$\frac{3}{5}$.
如图,在△ABC中,N为线段AC上靠近A点的四等分点,若$\overrightarrow{AP}$=(m+$\frac{1}{10}$)$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{BC}$,则m=$\frac{3}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com