
分析 (1)(i)求出函数的导数,求出导函数的递减区间,证出f(x)在此区间也递减即可;
(ii)法一:求出g(x),构造函数$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1$,求出其导数,根据函数的单调性通过比较判断即可;法二:将φ(x)变形为两个函数,通过函数的单调性判断即可;
(2)法一,根据(ii)中的法一分别求出x1,x2的范围,相加即可;法二,根据(ii)中的法二分别求出x1,x2的范围,相加即可.
解答 (1)证明:(i)因为$f(x)=a{x^4}-\frac{1}{2}{x^2}({x>0})$,所以f′(x)=4ax3-x,
由(4ax3-x)′=12ax2-1<0,得f′(x)的递减区间为$(0,\frac{1}{{2\sqrt{3a}}})$,…2 分
当$x∈(0,\frac{1}{{2\sqrt{3a}}})$时,f′(x)=4ax3-x=x(4ax2-1)<0,
所以f(x)在f′(x)的递减区间上也递减. …4 分
(ii)解法1:$g(x)=f(x)-f'(x)=a{x^4}-\frac{1}{2}{x^2}-(4a{x^3}-x)=a{x^4}-4a{x^3}-\frac{1}{2}{x^2}+x$,
因为x>0,由$g(x)=a{x^4}-4a{x^3}-\frac{1}{2}{x^2}+x=0$得$a{x^3}-4a{x^2}-\frac{1}{2}x+1=0$,
令$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1$,则$φ'(x)=3a{x^2}-8ax-\frac{1}{2}$,
因为a>0,且$φ'(0)=-\frac{1}{2}<0$,所以φ'(x)必有两个异号的零点,
记正零点为x0,则x∈(0,x0)时,φ'(x)<0,φ(x)单调递减;
x∈(x0,+∞)时,φ'(x)>0,φ(x)单调递增,
若φ(x)在(0,+∞)上恰有两个零点,则φ(x0)<0,…7 分
由$φ'({x_0})=3a{x_0}^2-8a{x_0}-\frac{1}{2}=0$得$3a{x_0}^2=8a{x_0}+\frac{1}{2}$,
所以$φ({x_0})=-\frac{32}{9}a{x_0}-\frac{1}{3}{x_0}+\frac{7}{9}$,又因为对称轴为$x=\frac{4}{3}$,
所以$φ(\frac{8}{3})=φ(0)=-\frac{1}{2}<0$,
所以${x_0}>\frac{8}{3}>\frac{7}{3}$,所以$φ({x_0})=-\frac{32}{9}a{x_0}-\frac{1}{3}({x_0}-\frac{7}{3})<0$,
又$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1=\frac{1}{2}a{x^2}(x-8)+\frac{1}{2}x(a{x^2}-1)+1$,
设$\frac{1}{{\sqrt{a}}},8$中的较大数为M,则φ(M)>0,
故a>0g(x)在(0,+∞)上恰有两个零点. …10 分
解法2:$g(x)=f(x)-f'(x)=a{x^4}-\frac{1}{2}{x^2}-(4a{x^3}-x)=a{x^4}-4a{x^3}-\frac{1}{2}{x^2}+x$,
因为x>0,由$g(x)=a{x^4}-4a{x^3}-\frac{1}{2}{x^2}+x=0$得$a{x^3}-4a{x^2}-\frac{1}{2}x+1=0$,
令$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1$,
若g(x)在(0,+∞)上恰有两个零点,则φ(x)在(0,+∞)上恰有两个零点,
当x=2时,由φ(x)=0得a=0,此时$φ(x)=-\frac{1}{2}x+1$在(0,+∞)上只有一个零点,不合题意;
当x≠2时,由$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1=0$得$\frac{1}{2a}=\frac{{{x^3}-4{x^2}}}{x-2}$,…7 分
令${φ_1}(x)=\frac{{{x^3}-4{x^2}}}{x-2}={x^2}-2x-4-\frac{8}{x-2}$,
则${φ'_1}(x)=\frac{{2x({x^2}-5x+8)}}{{{{(x-2)}^2}}}=\frac{{2x[{{(x-\frac{5}{2})}^2}+\frac{7}{4}]}}{{{{(x-2)}^2}}}>0$,
当x∈(0,2)时,φ(x)单调递增,且由$y={x^2}-2x-4,y=-\frac{8}{x-2}$值域知:φ(x)值域为(0,+∞);
当x∈(2,+∞)时,φ1(x)单调递增,且φ1(4)=0,
由$y={x^2}-2x-4,y=-\frac{8}{x-2}$值域知:φ(x)值域为(-∞,+∞);
因为a>0,所以$\frac{1}{2a}>0$,而$y=\frac{1}{2a}$与φ1(x)有两个交点,
所以φ1(x)在(0,+∞)上恰有两个零点. …10 分
(2)解法1:由(ii)知,对于$φ(x)=a{x^3}-4a{x^2}-\frac{1}{2}x+1$在(0,+∞)上恰有两个零点x1,x2,
不妨设x1<x2,又因为φ(0)=1>0,$φ(\frac{1}{2})=\frac{1}{8}(6-7a)<0$,
所以$0<{x_1}<\frac{1}{2}$,…12 分
又因为φ(4)=-1<0,$φ(\frac{9}{2})=\frac{1}{8}(657a-10)>0$,
所以$4<{x_2}<\frac{9}{2}$,
所以$4<{x_1}+{x_2}<\frac{1}{2}+\frac{9}{2}=5<a+4$. …16 分
解法2:由(ii)知$\frac{1}{2a}=\frac{{{x^3}-4{x^2}}}{x-2}$,
因为x∈[0,2)时,φ1(x)单调递增,$φ(\frac{1}{2})=\frac{7}{12}$,${φ_1}(0)=0<{φ_1}({x_1})=\frac{1}{2a}<{φ_1}(\frac{1}{2})$,
所以$0<{x_1}<\frac{1}{2}$,…12 分
当x∈(2,+∞)时,φ1(x)单调递增,${φ_1}(\frac{9}{2})=\frac{81}{20}$,${φ_1}(4)=0<{φ_1}({x_2})=\frac{1}{2a}<{φ_1}(\frac{9}{2})$,
所以$4<{x_2}<\frac{9}{2}$,
所以$4<{x_1}+{x_2}<\frac{1}{2}+\frac{9}{2}=5<a+4$. …16 分
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查不等式的证明,是一道难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | $\sqrt{41}$ | C. | $\sqrt{53}$ | D. | $\sqrt{45}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
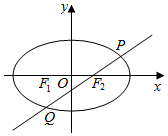 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1坐标为(-2,0),F2为椭圆C的右焦点,点M($\sqrt{3}$,1)在椭圆C上.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1坐标为(-2,0),F2为椭圆C的右焦点,点M($\sqrt{3}$,1)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [$\frac{31}{9}$,5] | C. | (2,+∞) | D. | ($\frac{31}{9}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
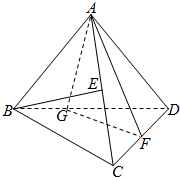 如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.
如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com