
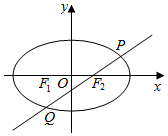
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1坐标为(-2,0),F2为椭圆C的右焦点,点M($\sqrt{3}$,1)在椭圆C上.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1坐标为(-2,0),F2为椭圆C的右焦点,点M($\sqrt{3}$,1)在椭圆C上.分析 (1)由已知求得c=2,再由点M($\sqrt{3}$,1)在椭圆C上,结合隐含条件求得a,b的值,则椭圆方程可求;
(2)①写出直线l的方程,与椭圆方程联立,利用弦长公式求得弦长;
②由条件知直线l斜率存在且不为零,设直线l方程为y=k(x-2),则直线F2T的方程为$y=-\frac{1}{k}(x-2)$,联立直线方程与椭圆方程,利用根与系数的关系求出N的坐标,得到ON的方程,由$\left\{\begin{array}{l}{y=-\frac{1}{k}(x-2)}\\{y=-\frac{1}{3k}x}\end{array}\right.$求得N的横坐标说明点T总在某定直线上.
解答 (1)解:由条件知c=2,则a2+b2=4,
∴椭圆C方程为$\frac{{x}^{2}}{{b}^{2}+4}+\frac{{y}^{2}}{{b}^{2}}=1$,
由点M($\sqrt{3}$,1)在椭圆C上,得$\frac{3}{{b}^{2}+4}+\frac{1}{{b}^{2}}=1$,解得b2=2(负值舍去).
∴椭圆C的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;
(2)①解:设点P(x1,y1),Q(x2,y2),
直线l:$y=\sqrt{3}(x-2)$,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\\{y=\sqrt{3}(x-2)}\end{array}\right.$,消去y得到5x2-18x+15=0,
此方程△≥0.
则${x}_{1}+{x}_{2}=\frac{18}{5},{x}_{1}{x}_{2}=3$.
则PQ=$\sqrt{1+(\sqrt{3})^{2}}|{x}_{1}-{x}_{2}|=2\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$2\sqrt{(\frac{18}{5})^{2}-12}=\frac{4\sqrt{6}}{5}$.
由PF1+PF2+QF1+QF2=4a,得PF1+QF1=4a-(PF2+QF2)=$\frac{16\sqrt{6}}{5}$;
②证明:由条件知直线l斜率存在且不为零,设直线l方程为y=k(x-2),
则直线F2T的方程为$y=-\frac{1}{k}(x-2)$.
由$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{2}=1\\ y=k(x-2)\end{array}\right.$,消去y得到(1+3k2)x2-12k+12k2-6=0,此方程△≥0.
则${x_1}+{x_2}=\frac{{12{k^2}}}{{1+3{k^2}}}$,${x_1}{x_2}=\frac{{12{k^2}-6}}{{1+3{k^2}}}$
∴y1+y2=k(x1+x2)-4k=$k•\frac{12{k}^{2}}{1+3{k}^{2}}-4k=\frac{-4k}{1+3{k}^{2}}$.
∴点$N(\frac{6{k}^{2}}{1+3{k}^{2}},\frac{-2k}{1+3{k}^{2}})$,
∴直线ON斜率为$\frac{\frac{-2k}{1+3{k}^{2}}}{\frac{6{k}^{2}}{1+3{k}^{2}}}=-\frac{1}{3k}$.
直线ON方程为$y=\frac{1}{-3k}x$.
由$\left\{\begin{array}{l}{y=-\frac{1}{k}(x-2)}\\{y=-\frac{1}{3k}x}\end{array}\right.$,得到$-\frac{1}{k}(x-2)=-\frac{1}{3k}x$,解得x=3.则T横坐标为定值3.
∴点T恒在直线x=3上.
点评 本题考查椭圆标准方程的求法,考查了直线与椭圆位置关系的应用,训练了利用弦长公式求弦长,考查恒过定点问题的求解方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 400 | B. | 360 | C. | 200 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国古代数学名著《九章算术》中的更相减损法的思路与图相似.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
我国古代数学名著《九章算术》中的更相减损法的思路与图相似.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com