
分析 由函数零点的定义设出f(x)的解析式,结合条件求出顶点坐标,代入函数解析式求出系数,即可求出f(x)的解析式,由配方法和二次函数的性质求出值域.
解答 解:∵二次函数y=f(x)的两个零点为0,1,
∴设f(x)=ax(x-1),则定点的横坐标x=$\frac{1}{2}$,
∵f(x)图象的顶点恰好在函数y=log2x的图象上,
∴y=log2$\frac{1}{2}$=-1,则顶点为$(\frac{1}{2},-1)$,
代入f(x)得,$\frac{1}{2}$a($\frac{1}{2}$-1)=-1,解得a=4,
则f(x)=4x(x-1)=4$(x-\frac{1}{4})^{2}-1$,
∵x∈[0,2],
∴当x=$\frac{1}{4}$时,f(x)取到最小值是-1;当x=2时,f(x)取到最大值是8,
∴-1≤f(x)≤8,即f(x)的值域是[-1,8].
点评 本题考查函数零点的定义,待定系数法求出函数解析式,以及二次函数的性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | $\sqrt{41}$ | C. | $\sqrt{53}$ | D. | $\sqrt{45}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
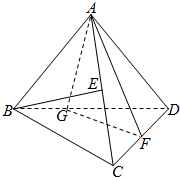 如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.
如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,$BD=4\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
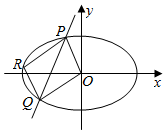 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x0)=0 | B. | f(x0)<0 | C. | f(x0)>0 | D. | f(x0)的符号不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com