
分析 (I)设出A,B,D三点坐标,根据kBD=y′|${\;}_{x={x}_{A}}$列方程.根据根与系数的关系求出M的横坐标即可;
(II)求出直线BD的方程,求出AM和B到直线AM的距离,则S△ABD=2S△ABM,求出S关于xA的函数,利用基本不等式求出函数的最小值.
解答 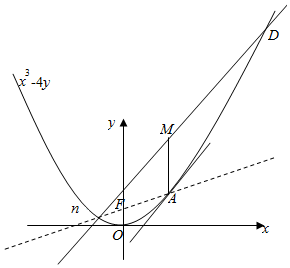 证明:(Ⅰ)设A(x0,$\frac{{{x}_{0}}^{2}}{4}$),B(x1,$\frac{{{x}_{1}}^{2}}{4}$),D(x2,$\frac{{{x}_{2}}^{2}}{4}$).(x0>0)
证明:(Ⅰ)设A(x0,$\frac{{{x}_{0}}^{2}}{4}$),B(x1,$\frac{{{x}_{1}}^{2}}{4}$),D(x2,$\frac{{{x}_{2}}^{2}}{4}$).(x0>0)
由x2=4y得y=$\frac{{x}^{2}}{4}$,
∴y′=$\frac{x}{2}$,
∴kBD=$\frac{x0}{2}$,
又kBD=$\frac{\frac{{{x}_{2}}^{2}}{4}-\frac{{{x}_{1}}^{2}}{4}}{{x}_{2}-{x}_{1}}$=$\frac{x1+x2}{4}$,
∴$\frac{x0}{2}$=$\frac{x1+x2}{4}$,
∴$\frac{{x}_{1}+{x}_{2}}{2}$=x0,即xM=x0.
∴AM与y轴平行.
解:(Ⅱ)F(0,1),
∴kAF=$\frac{\frac{{{x}_{0}}^{2}}{4}-1}{{x}_{0}}$=$\frac{{x}_{0}}{4}-\frac{1}{{x}_{0}}$,kBF=$\frac{\frac{{{x}_{1}}^{2}}{4}-1}{{x}_{1}}$=$\frac{{x}_{1}}{4}-\frac{1}{{x}_{1}}$.
∵A,B,F三点共线,
∴kAF=kBF,
∴$\frac{{x}_{0}}{4}-\frac{1}{{x}_{0}}$=$\frac{{x}_{1}}{4}-\frac{1}{{x}_{1}}$,整理得(x0x1+4)(x0-x1)=0,
∵x0-x1≠0,
∴x0x1=-4,即x1=-$\frac{4}{x0}$.
直线BD的方程为y=$\frac{x0}{2}$(x-x1)+$\frac{{{x}_{1}}^{2}}{4}$,
∴yM=$\frac{{x}_{0}}{2}$(x0-x1)+$\frac{{{x}_{1}}^{2}}{4}$=$\frac{{{x}_{0}}^{2}}{2}$+$\frac{{{x}_{1}}^{2}}{4}$+2=$\frac{{{x}_{0}}^{2}}{2}$+$\frac{4}{{{x}_{0}}^{2}}$+2.
由(Ⅰ)得S△ABD=2S△ABM=|$\frac{{{x}_{0}}^{2}}{2}$+$\frac{4}{{{x}_{0}}^{2}}$+2-$\frac{{{x}_{0}}^{2}}{4}$|×|x1-x0|
=|$\frac{{{x}_{0}}^{2}}{4}$+$\frac{4}{{{x}_{0}}^{2}}$+2|×|x0+$\frac{4}{x0}$|=$\frac{1}{4}$(x0+$\frac{4}{x0}$)3≥16,
当且仅当x0=$\frac{4}{x0}$即x0=2时等号成立,
∴S的最小值为16.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,N为线段AC上靠近A点的四等分点,若$\overrightarrow{AP}$=(m+$\frac{1}{10}$)$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{BC}$,则m=$\frac{3}{5}$.
如图,在△ABC中,N为线段AC上靠近A点的四等分点,若$\overrightarrow{AP}$=(m+$\frac{1}{10}$)$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{BC}$,则m=$\frac{3}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos(x+$\frac{π}{4}$)cos(x-$\frac{π}{4}$),x∈R
已知函数f(x)=sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos(x+$\frac{π}{4}$)cos(x-$\frac{π}{4}$),x∈R查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
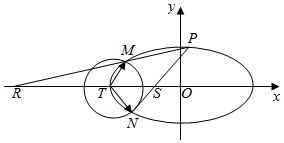 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\int_{\;\;0}^{\;\;1}$xdx | B. | $\int_{\;\;0}^{\;\;1}{{e^x}$dx | C. | $\int_{\;\;0}^{\;\;\frac{π}{2}}$1dx | D. | $\int_{\;\;0}^{\;\;\frac{π}{2}}$cosxdx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com