
【题目】已知数列{an}的前n项和为Sn,满足Sn=2an-1.(n∈N*)
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足bn=![]() an,求数列{bn}的前n项和Tn.
an,求数列{bn}的前n项和Tn.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上存在一点
上存在一点![]()
![]() 到焦点
到焦点![]() 的距离等于
的距离等于![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点在
两点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求△
,求△![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在D上的函数,若对D中的任意两数
是定义在D上的函数,若对D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的C函数.
为定义在D上的C函数.
(1)试判断函数![]() 是否为定义域上的C函数,并说明理由;
是否为定义域上的C函数,并说明理由;
(2)若函数![]() 是R上的奇函数,试证明
是R上的奇函数,试证明![]() 不是R上的C函数;
不是R上的C函数;
(3)设![]() 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数![]() 以及D中的任意两数
以及D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的π函数. 已知
为定义在D上的π函数. 已知![]() 是R上的π函数,m是给定的正整数,设
是R上的π函数,m是给定的正整数,设![]() ,且
,且![]() ,记
,记![]() . 对于满足条件的任意函数
. 对于满足条件的任意函数![]() ,试求
,试求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
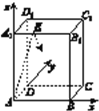
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列a1,a2……an是正整数1,2,……,n的任一排列,且同时满足以下两个条件:
①a1=1;②当n≥2时,|ai-ai+1|≤2(i=1,2,…,n-1).
记这样的数列个数为f(n).
(I)写出f(2),f(3),f(4)的值;
(II)证明f(2018)不能被4整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 是曲线
是曲线![]() 与直线
与直线![]() :
: ![]() (
(![]() )的交点(异于原点
)的交点(异于原点![]() ).
).
(1)写出![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)求过点![]() 和直线
和直线![]() 垂直的直线
垂直的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·南充调研)如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖立放置在同一水平线上,则大致的图形是( )
A. 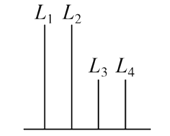 B.
B. 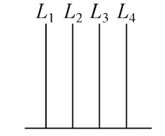
C. 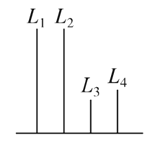 D.
D. 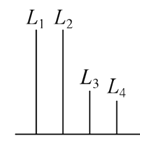
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com