
分析 (Ⅰ)根据绝对值的意义求出f(x)的最小值,从而求出a的范围即可;(Ⅱ)求出g(x)的最小值,问题转化为解不等式|2m-1|-|m+1|≥3即可.
解答 解:(Ⅰ)函数f(x)=|2x-1|+|2x+3|≥|2x-1-2x-3|=4,
若对任意的实数x,关于x的不等式f(x)≥a恒成立,
∴a≤4;
(Ⅱ)g(x)=f(x)-|2x+3|-|x+1|=|2x-1|-|x+1|,
x<-1时:g(x)=-(2x-1)+(x+1)=-x+2,
在x∈(-∞,-1)上,g(x)>3,
故若存在x<-1,使g(x)≤g(m)成立,
只需g(m)≥3即可,
转化为解不等式|2m-1|-|m+1|≥3,
不等式可化为:$\left\{\begin{array}{l}{m≤-1}\\{-m+2≥3}\end{array}\right.$或$\left\{\begin{array}{l}{-1<m<\frac{1}{2}}\\{-3m≥3}\end{array}\right.$或$\left\{\begin{array}{l}{m≥\frac{1}{2}}\\{m-2≥3}\end{array}\right.$,
解得:m≤-1或m≥5.
点评 本题考察了函数恒成立问题,考察解绝对值不等式问题,考察分类讨论思想,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
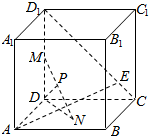 已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.
已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
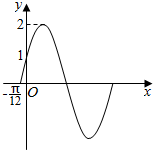 能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com