
分析 (1)由条件便得到方程ax2+(b-1)x+c+1=0有两个实根1,2,根据韦达定理便可得出b=1-3a,c=2a-1,从而由f(x)>0可得到$a(x-\frac{2a-1}{a})(x-1)>0$,为解该不等式,从而需讨论a>0和a<0,以及$\frac{2a-1}{a}$和1的关系,从而解出该不等式,即得出f(x)>0的解集;
(2)根据条件便得到一元二次方程ax2+(b-1)x+c=0有二重根1,由韦达定理便可得到b=1-2a,c=a,从而得出f(x)=ax2+(1-2a)x+a,可求出f(x)的对称轴$x=1-\frac{1}{2a}<1$,从而可讨论$1-\frac{1}{2a}<0$和$1-\frac{1}{2a}≥0$两种情况,可以求出每种情况下f(x)在[-2,2]上的最大值,这样便可得出f(x)在[-2,2]上的最大值M(a).
解答 解:(1)根据题意知方程ax2+bx+c=x-1有两个实根1,2;
即方程ax2+(b-1)x+c+1=0有两个实根1,2;
∴$\left\{\begin{array}{l}{1+2=-\frac{b-1}{a}}\\{1•2=\frac{c+1}{a}}\end{array}\right.$;
∴b=1-3a,c=2a-1;
∴f(x)=ax2+(1-3a)x+2a-1=[ax-(2a-1)]•(x-1);
∴由f(x)>0得[ax-(2a-1)](x-1)>0;
即$a(x-\frac{2a-1}{a})(x-1)>0$(Ⅰ);
①若a>0,上面不等式变成$(x-\frac{2a-1}{a})(x-1)>0$;
1)当$\frac{2a-1}{a}>1$,即a>1时,上面不等式即不等式f(x)>0的解集为(-∞,1)∪($\frac{2a-1}{a}$,+∞);
2)当$\frac{2a-1}{a}=1$,即a=1时,f(x)>0的解集为{x|x≠1};
3)当$\frac{2a-1}{a}<1$,即0<a<1时,f(x)>0的解集为$(-∞,\frac{2a-1}{a})∪(1,+∞)$;
②若a<0,不等式(Ⅰ)变成$(x-\frac{2a-1}{a})(x-1)<0$;
a<0;
∴$\frac{2a-1}{a}=2-\frac{1}{a}>1$;
∴f(x)>0的解集为$(1,\frac{2a-1}{a})$;
(2)由条件知方程ax2+bx+c=x有二重根1;
即方程ax2+(b-1)x+c=0有二重根1;
∴$\left\{\begin{array}{l}{1+1=-\frac{b-1}{a}}\\{1•1=\frac{c}{a}}\end{array}\right.$;
∴b=1-2a,c=a;
∴f(x)=ax2+(1-2a)x+a;
a>0,f(x)的对称轴为x=$\frac{2a-1}{2a}$=$1-\frac{1}{2a}<1$;
∴①$1-\frac{1}{2a}<0$,即$0<a<\frac{1}{2}$时,x=2时,f(x)在[-2,2]上取到最大值a+2;
②$1-\frac{1}{2a}≥0$,即$a≥\frac{1}{2}$时,x=-2时,f(x)在[-2,2]上取到最大值9a-2;
∴$M(a)=\left\{\begin{array}{l}{a+2}&{0<a<\frac{1}{2}}\\{9a-2}&{a≥\frac{1}{2}}\end{array}\right.$.
点评 考查描述法表示集合,韦达定理,以及一元二次不等式的解法,二次函数的对称轴,二次函数的最大值,要熟悉二次函数的图象.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 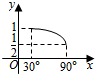 | B. | 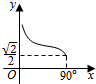 | C. | 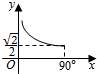 | D. | 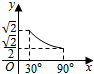 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com