
分析 ①由y=-2cos($\frac{7}{2}$π-2x)=2sin2x,得出y是定义域R上的奇函数;
②举例说明命题错误即可;
③x=-$\frac{3π}{8}$时函数y取得最值,即得x=-$\frac{3π}{8}$是函数y的一条对称轴;
④化简函数y,求出函数y的单调减区间即可.
解答 解:对于①,y=-2cos($\frac{7}{2}$π-2x)=2sin2x,是定义域R上的奇函数,命题正确;
对于②,α,β是第一象限角,且α=390°>β=30°,则sinα=sinβ,原命题错误;
对于③,x=-$\frac{3π}{8}$时,函数y=3sin(2x-$\frac{3π}{4}$)=3sin(2×(-$\frac{3π}{8}$)-$\frac{3π}{4}$)=3取得最大值,
∴x=-$\frac{3π}{8}$是函数y=3sin(2x-$\frac{3π}{4}$)的一条对称轴,命题正确;
对于④,函数y=sin($\frac{π}{4}$-2x)=-sin(2x-$\frac{π}{4}$),
令-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{4}$≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{π}{8}$+kπ≤x≤$\frac{3π}{8}$+kπ,k∈Z,
∴y=sin($\frac{π}{4}$-2x)的单调减区间是[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z),命题正确;
综上,正确的命题序号是①③④.
故答案为:①③④.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了命题真假的判断问题,是基础题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
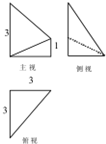
| A. | 18cm3 | B. | 6cm3 | C. | $\frac{9}{2}c{m^3}$ | D. | $\frac{27}{2}c{m^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
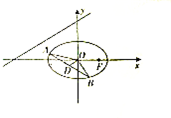 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,右焦点F到直线x=$\frac{a^2}{c}$的距离为1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
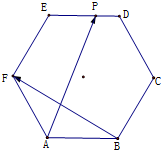 如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..
如图,正六边形ABCDEF的边长为2,P是线段DE上的任意一点,则$\overrightarrow{AP}$•$\overrightarrow{BF}$的取值范围为[0,6]..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | $[0,2)∪\{-\frac{18}{e^2}\}$ | C. | $(0,2)∪\{-\frac{18}{e^2}\}$ | D. | $[0,2\sqrt{e})∪\{-\frac{18}{e^2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.
如图,在四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,且AB=4,BC=CD=ED=EA=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(万千瓦时) | 2.5 | 2 | 1.5 | 2 | 2.5 | 2 | 1.5 | 2 | 2.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.5 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 0.1 | B. | 0.05 | C. | 0.025 | D. | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com