
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(万千瓦时) | 2.5 | 2 | 1.5 | 2 | 2.5 | 2 | 1.5 | 2 | 2.5 |
分析 (Ⅰ)观察表中数据,可得周期T=12,从而ω=$\frac{π}{6}$,根据三角函数的最值特点,求取A,B的值,选取一个坐标即可得到函数y=Asin(ωt+φ)+B,
(Ⅱ)利用三角函数的性质,求其在范围的情况,
解答 解:观察表中数据,可得周期T=12,从而ω=$\frac{π}{6}$,
由:$\left\{\begin{array}{l}{A+B=2.5}\\{-A+B=1.5}\end{array}\right.$,解得:A=0.5,B=2.
所以:函数y=0.5sin($\frac{π}{6}$t+φ)+2.
又函数y=0.5sin($\frac{π}{6}$t+φ)+2过坐标(0,2.5),带入解得:φ=$\frac{π}{2}+2kπ$,(k∈Z);
∵0<φ<π;
∴φ=$\frac{π}{2}$.
故:所求函数解析式为y=0.5sin($\frac{π}{6}$t$+\frac{π}{2}$)+2.(0≤t≤24).
(Ⅱ)由题意,可知,0.5sin($\frac{π}{6}$t$+\frac{π}{2}$)+2>2.25.
解得:cos$\frac{π}{6}t$>$\frac{1}{2}$,即$-\frac{π}{3}+2kπ<\frac{π}{6}t<\frac{π}{3}+$2kπ,(k∈Z).
整理得:-2+12k<t<2+12k,(k∈Z).
∵0≤t≤24,
令k=0,1,3…24.
当k=0时,0≤t<2;
当k=1时,10<t<14;
当k=2时,22<t≤24.
∴在一天内的上午8:00到下午18:00,有4个小时要提高企业电价.
点评 本题主要考查三角函数的图象和性质,根据表中的数据特点求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| Y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 0 | B. | 2.2 | C. | 2.6 | D. | 3.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | 2016 | C. | 504 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
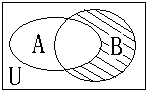
| A. | (∁UA)∩B | B. | (∁UA)∩(CUB) | C. | A∩(∁UB) | D. | A∪(∁UB) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com