
分析 (1)利用倍角公式化弦为切证明;
(2)写出两角和与差的正弦,作和证得答案;
(3)在(2)的基础上,令α+β=θ,α-β=φ,解得:α=$\frac{θ+φ}{2}$,β=$\frac{θ-φ}{2}$.代回cosαsinβ=$\frac{1}{2}$[sin(α+β)-sin(α-β)],则可证明结论成立.
解答 证明:(1)∵$\frac{sinα}{1+cosα}=\frac{2sin\frac{α}{2}cos\frac{α}{2}}{2co{s}^{2}\frac{α}{2}}=\frac{sin\frac{α}{2}}{cos\frac{α}{2}}=tan\frac{α}{2}$,
∴tan$\frac{α}{2}$=$\frac{sinα}{1+cosα}$;
又$\frac{1-cosα}{sinα}$=$\frac{2si{n}^{2}\frac{α}{2}}{2sin\frac{α}{2}cos\frac{α}{2}}=\frac{sin\frac{α}{2}}{cos\frac{α}{2}}=tan\frac{α}{2}$,
∴$\frac{sinα}{1+cosα}$=$\frac{1-cosα}{sinα}$;
(2)∵sin(α+β)=sinαcosβ+cosαsinβ ①,
sin(α-β)=sinαcosβ-cosαsinβ ②,
①-②得:cosαsinβ=$\frac{1}{2}$[sin(α+β)-sin(α-β)];
(3)由(2)知,cosαsinβ=$\frac{1}{2}$[sin(α+β)-sin(α-β)]③.
令α+β=θ,α-β=φ,解得:α=$\frac{θ+φ}{2}$,β=$\frac{θ-φ}{2}$.
代入上式可得:sinθ-sinφ=cos$\frac{θ+φ}{2}$$•sin\frac{θ-φ}{2}$.
即sinα-sinβ=2cos$\frac{α+β}{2}$sin$\frac{α-β}{2}$.
点评 本题考查三角函数恒等式的证明,关键是对同角三角函数基本关系式和两角和与差的正弦的灵活运用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (1,2) | C. | -7 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2016π}$ | B. | $\frac{1}{4032π}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{4032}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
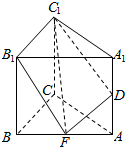 如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )
如图,已知直三棱柱ABC-A1B1C1的侧棱长是2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积是( )| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com