考点:直线与圆的位置关系
专题:直线与圆
分析:在①中,直线l的方程可化为y=
x-,从而直线l的斜率k的取值范围是[0,
],由此得到直线l的倾斜角不是钝角;
在②中,由直线l的方程为:y=k(x-4),其中0≤k
≤,得当k=0或k=
时,直线l不过第一、三、四象限;
在③中,圆心C到直线l的距离d≥
>1,从而直线l与圆C相交,圆C截直线l所得的弦所对的圆心角小于
,从而直线l不能将圆C分割成弧长的比值为
的两段弧;
④由圆心C到直线l的距离d≥
,得直线l与圆C相交的最大弦长为
.
解答:
解:在①中,直线l的方程可化为y=
x-,
于是直线l的斜率k=
,
∵|m|≤
(m2+1),∴|k|=
≤,
当且仅当|m|=1时等号成立.
∵m≥0,
∴直线l的斜率k的取值范围是[0,
],
∴直线l的倾斜角不是钝角,故①正确;
在②中,∵直线l的方程为:y=k(x-4),其中0≤k
≤,
∴当k=0或k=
时,直线l不过第一、三、四象限,故②错误;
在③中,直线l的方程为:y=k(x-4),其中0≤k
≤,
圆C的方程可化为(x-4)
2+(y+2)
2=4,
∴圆C的圆心为C(4,-2),半径r=2,
于是圆心C到直线l的距离d=
,
由0≤k
≤,得d≥
>1,即d>
,
∴若直线l与圆C相交,
则圆C截直线l所得的弦所对的圆心角小于
,
故直线l不能将圆C分割成弧长的比值为
的两段弧,故③错误;
由③知圆心C到直线l的距离d≥
,
∴直线l与圆C相交的最大弦长为:2
=
,故④正确.
故答案为:①④.
点评:本题考查圆的性质和直线与圆的位置关系的应用,解题时要认真审题,是中档题.



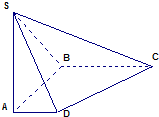 在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<
在四棱锥S-ABCD中,SA⊥底面ABCD,AD⊥AB,AD∥BC,AD=1,AB=BC=2,cos<