
分析 由题意对已知函数求两次导数可得图象关于点($\frac{1}{2}$,1)对称,即f(x)+f(1-x)=2,即可得到结论.
解答 解:(1)函数的导数f′(x)=x2-x+3,
f″(x)=2x-1,
由f″(x0)=0得2x0-1=0
解得x0=$\frac{1}{2}$,而f($\frac{1}{2}$)=1,
故函数g(x)关于点($\frac{1}{2}$,1)对称,
(2)由(1)知f(x)+f(1-x)=2,
∴f($\frac{1}{2003}$)+f($\frac{2012}{2013}$)=f($\frac{2}{2013}$+$\frac{2011}{2013}$)=…=f($\frac{1006}{2013}$)+f($\frac{1007}{2013}$),
∴$f({\frac{1}{2013}})+$$f({\frac{2}{2013}})+$$f({\frac{3}{2013}})+$$f({\frac{4}{2013}})+$…$+f({\frac{2012}{2013}})$=2012.
点评 本题是新定义题,考查了函数导函数的零点的求法,考查了函数的性质,解答的关键是寻找函数值所满足的规律,是中档题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 因为∠A和∠B是两条平行直线被第三条直线所截得的同旁内角,所以∠A+∠B=180° | |
| B. | 我国地质学家李四光发现中国松辽地区和中亚细亚的地质结构类似,而中亚细亚有丰富的石油,由此,他推断松辽平原也蕴藏着丰富的石油 | |
| C. | 由6=3+3,8=3+5,10=3+7,12=5+7,14=7+7,…,得出结论:一个偶数(大于4)可以写成两个素数的和 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),通过计算a2,a3,a4,a5的值归纳出{an}的通项公式 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
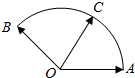 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com