
某分公司经销某种品牌产品,每件产品的成本为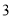 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交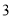 元的管理费,预计当每件产品的售价为
元的管理费,预计当每件产品的售价为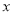 元(
元(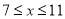 )时,一年的销售量为
)时,一年的销售量为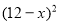 万件.
万件.
(1)求该分公司一年的利润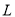 (万元)与每件产品的售价
(万元)与每件产品的售价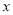 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,该分公司一年的利润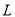 最大?并求出
最大?并求出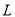 的最大值.
的最大值.
(1)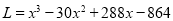 ,
,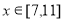 ;(2)当每件产品的售价
;(2)当每件产品的售价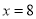 时,该分公司一年的利润最大,且最大利润
时,该分公司一年的利润最大,且最大利润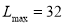 万元.
万元.
【解析】
试题分析:(1)解实际应用题,关键是正确理解题意,正确列出等量关系或函数关系式.本题中利润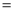 每件产品的利润
每件产品的利润 销售量,进而根据已知即可得出该分公司一年的利润
销售量,进而根据已知即可得出该分公司一年的利润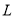 与每件产品的售价
与每件产品的售价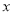 的函数关系式;(2)根据(1)中确定的函数关系式,由函数的最值与函数的导数的关系,求出该函数的最大值即可.
的函数关系式;(2)根据(1)中确定的函数关系式,由函数的最值与函数的导数的关系,求出该函数的最大值即可.
(1)分公司一年的利润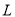 (万元)与售价
(万元)与售价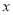 的函数关系式为
的函数关系式为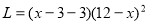
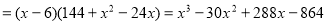 ,
,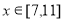 6分
6分
(2)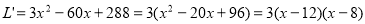
令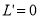 ,得
,得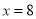 或
或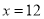 (不合题意,舍去) 8分
(不合题意,舍去) 8分
当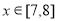 时,
时,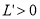 ,
,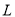 单调递增;当
单调递增;当 时,
时,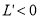 ,
,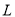 单调递减 10分
单调递减 10分
于是:当每件产品的售价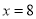 时,该分公司一年的利润最大,且最大利润
时,该分公司一年的利润最大,且最大利润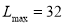 万元 12分
万元 12分
考点:导数的实际应用.


科目:高中数学 来源:2015届陕西省咸阳市高二下学期期末质量检测文科数学试卷(解析版) 题型:选择题
设原命题:若a+b≥2,则a,b中至少有一个不小于1,则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
查看答案和解析>>
科目:高中数学 来源:2015届重庆市高二下期期中考试文科数学试卷(解析版) 题型:选择题
在独立性检验中,统计量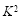 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当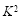 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当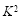 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当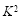
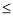 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的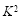 =20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
=20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
A.有95%的把握认为两者有关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源:2015届重庆市高二下学期期中考试理科数学试卷(解析版) 题型:选择题
如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有( )
A.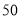 种 B.
种 B.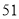 种 C.
种 C.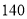 种 D.
种 D.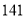 种
种
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
(可能用到的公式: ,
,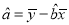 ,其中
,其中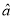 、
、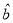 是对回归直线方程
是对回归直线方程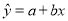 中系数
中系数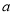 、
、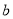 按最小二乘法求得的估计值)
按最小二乘法求得的估计值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com