
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-5x+6=0则x=2”的逆否命题是“若x≠2则x2-5x+6≠0” | |
| B. | 命题“已知x、y∈R,若x+y≠3,则x≠2或y≠1是真命题” | |
| C. | 已知命题p和q,若p∨q为真命题,则命题p与q中必一真一假 | |
| D. | 命题p:?x0∈R,x02+x0+1<0,则¬p:?x0∈R,x02+x0+1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
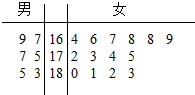 某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.
某航空公司在2015年年初招收了20名空乘人员(服务员与空警),其中“男性空乘人员”6名,“女性空乘人员”14名,并对他们的身高进行了测量,其身高(单位:cm)的茎叶图如图所示.公司决定:身高在170以上(包含170cm)的进入“国际航班”做空乘人员,身高在170cm以下的进入“国内航班”做空乘人员.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=kx+h | B. | f(x)=ax2+bx+c | C. | f(x)=pqx+r | D. | f(x)=mlnx+n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com