
分析 (1)把要求得不等式去掉绝对值,化为与之等价的3个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(2)由条件可得-$\frac{3a}{2(x-y)}$+$\frac{b}{4(y-z)}$>$\frac{2}{x-z}$>$\frac{1}{x-z}$,从而证得结论,可得k的最大值为2.
解答 解:(1)由不等式|2x-1|-|x+1|<2,可得$\left\{\begin{array}{l}{x<-1}\\{1-2x-(-x-1)<2}\end{array}\right.$①,或$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{1-2x-(x+1)<2}\end{array}\right.$,
或 $\left\{\begin{array}{l}{x>\frac{1}{2}}\\{2x-1-(x+1)<2}\end{array}\right.$ ③.
解①求的x∈∅,解②求得-$\frac{2}{3}$<x≤$\frac{1}{2}$,解③求得$\frac{1}{2}$<x<4,
综上可得,-$\frac{2}{3}$<x<4.
再根据不等式的解集为{x|a<x<b},可得a=-$\frac{2}{3}$,b=4.
(2)∵x>y>z,∴x-y>0,y-z>0,x-z>0,
∴-$\frac{3a}{2(x-y)}$+$\frac{b}{4(y-z)}$=$\frac{2}{2(x-y)}$+$\frac{4}{4(y-z)}$=$\frac{1}{x-y}$+$\frac{1}{y-z}$>$\frac{1}{x-z}$+$\frac{1}{x-z}$=$\frac{2}{x-z}$>$\frac{1}{x-z}$,
故存在实数k使-$\frac{3a}{2(x-y)}$+$\frac{b}{4(y-z)}$≥$\frac{k}{x-z}$恒成立.
由以上可得,k的最大值为2.
点评 本题主要考查绝对值不等式的解法,不等式的性质应用,属于中档题.


科目:高中数学 来源: 题型:填空题
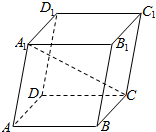 如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.
如图所示的平行六面体ABCD-A1B1C1D中,AB=AD=AA1=1,∠BAD=90°,∠BAA1=∠DAA1=60°,则CA1的长=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}-{y^2}=1$ | B. | ${y^2}-\frac{x^2}{2}=1$ | C. | ${x^2}-{\frac{y}{2}^2}=1$ | D. | $\frac{y^2}{2}-{x^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com