
【题目】已知函数![]() ,
, ![]() .
.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )若对任意
)若对任意![]() ,
, ![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(![]() )单调增区间为
)单调增区间为![]() ,单调减区间
,单调减区间![]() 和
和![]() .(
.(![]() )
)![]() .
.
【解析】试题分析:(1)求出函数的导数 ,解不等式,求出函数的单调区间即可;
,解不等式,求出函数的单调区间即可;
(2)问题等价于“对于任意![]() ,
, ![]() 恒成立”.分
恒成立”.分![]() ,
, ![]() 讨论函数的单调性求出a的范围即可.
讨论函数的单调性求出a的范围即可.
试题解析:(![]() )
)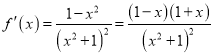 .
.
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() 或
或![]() .
.
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间
,单调减区间![]() 和
和![]() .
.
(![]() )依题意,“对于任意
)依题意,“对于任意![]() ,
, ![]() ,
, ![]() 恒成立”等价于“对于任意
恒成立”等价于“对于任意![]() ,
, ![]() 恒成立”.
恒成立”.
由(![]() )知,函数
)知,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∵![]() ,
, ![]() ,∴函数
,∴函数![]() 的最小值为
的最小值为![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,令
,令![]() ,得
,得![]() ,
, ![]() .
.
①当![]() ,即
,即![]() 时,当
时,当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,
∴函数![]() .
.
由![]() 得,
得, ![]() ,
,
∴![]() .
.
②当![]() ,即
,即![]() 时,
时, ![]() 时
时![]() ,
, ![]() 时,
时, ![]() ,
,
∴函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() .
.
由![]() 得,
得, ![]() ,
,
∴![]() .
.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,平面
为菱形,平面![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
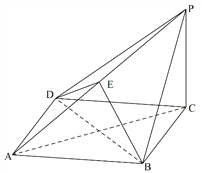
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的
的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(CCTV-1)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课。每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 两个地区的
两个地区的![]() 名观众,得到如下的
名观众,得到如下的![]() 列联表:
列联表:
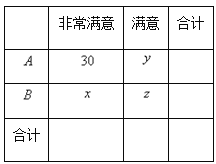
已知在被调查的![]() 名观众中随机抽取
名观众中随机抽取![]() 名,该观众是
名,该观众是![]() 地区当中“非常满意”的观众的概率为
地区当中“非常满意”的观众的概率为![]() ,且
,且![]() .
.
(1)现从![]() 名观众中用分层抽样的方法抽取
名观众中用分层抽样的方法抽取![]() 名进行问卷调查,则应抽取“满意”的
名进行问卷调查,则应抽取“满意”的![]() 地区的人数各是多少.
地区的人数各是多少.
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取
地区随机抽取![]() 人,设抽到的观众“非常满意”的人数为
人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
|
|
|
|
|
|
|
|
附:参考公式:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是等差数列,
是等差数列,![]() ,
,![]() 是等比数列,
是等比数列,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若 ,求当
,求当![]() 是偶数时,数列
是偶数时,数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若![]() ,是否存在实数
,是否存在实数![]() 使得不等式
使得不等式![]() 对任意的
对任意的![]() ,
,![]() 恒成立?若存在,求出所有满足条件的实数
恒成立?若存在,求出所有满足条件的实数![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以![]() 元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以
元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂某天购进了80斤米粉,以![]() (单位:斤)(其中
(单位:斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (单位:元)表示利润.
(单位:元)表示利润.
(Ⅰ)计算当天米粉需求量的平均数,并直接写出需求量的众数和中位数;
(Ⅱ) 将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅲ)根据直方图估计该天食堂利润不少于760元的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com