
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
【答案】(1)![]() ;(2)直线AB过定点Q(0,﹣2).
;(2)直线AB过定点Q(0,﹣2).
【解析】试题分析:(1)根据椭圆的几何性质得到椭圆方程;(2)先由特殊情况得到结果,再考虑一般情况,联立直线和椭圆得到二次函数,根据韦达定理,和向量坐标化的方法,得到结果。
(Ⅰ)由椭圆的离心率e=![]() ,则a2=4b2, 将P(2,1)代入椭圆
,则a2=4b2, 将P(2,1)代入椭圆![]() ,则
,则![]() ,解得:b2=2,则a2=8, ∴椭圆的方程为:
,解得:b2=2,则a2=8, ∴椭圆的方程为: ![]() ;
;
(Ⅱ)当M,N分别是短轴的端点时,显然直线AB为y轴,所以若直线过定点,这个定点一点在y轴上,
当M,N不是短轴的端点时,设直线AB的方程为y=kx+t,设A(x1,y1)、B(x2,y2),
由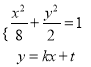 消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
消去y得(1+4k2)x2+8ktx+4t2﹣8=0,·则△=16(8k2﹣t2+2)>0,
x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
又直线PA的方程为y﹣1=![]() (x﹣2),即y﹣1=
(x﹣2),即y﹣1=![]() (x﹣2),
(x﹣2),
因此M点坐标为(0, ![]() ),同理可知:N(0,
),同理可知:N(0, ![]() ),
),
由![]() ,则
,则![]() +
+![]() =0,
=0,
化简整理得:(2﹣4k)x1x2﹣(2﹣4k+2t)(x1+x2)+8t=0,
则(2﹣4k)×![]() ﹣(2﹣4k+2t)(
﹣(2﹣4k+2t)(![]() )+8t=0,
)+8t=0,
当且仅当t=﹣2时,对任意的k都成立,直线AB过定点Q(0,﹣2).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
已知曲线C![]() :
:![]() (t为参数), C
(t为参数), C![]() :
:![]() (
(![]() 为参数)。
为参数)。
(1)化C![]() ,C
,C![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为C
,Q为C![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线
![]() (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着现代社会的发展,我国对于环境保护越来越重视,企业的环保意识也越来越强.现某大型企业为此建立了5套环境监测系统,并制定如下方案:每年企业的环境监测费用预算定为1200万元,日常全天候开启3套环境监测系统,若至少有2套系统监测出排放超标,则立即检查污染源处理系统;若有且只有1套系统监测出排放超标,则立即同时启动另外2套系统进行1小时的监测,且后启动的这2套监测系统中只要有1套系统监测出排放超标,也立即检查污染源处理系统.设每个时间段(以1小时为计量单位)被每套系统监测出排放超标的概率均为![]() ,且各个时间段每套系统监测出排放超标情况相互独立.
,且各个时间段每套系统监测出排放超标情况相互独立.
(1)当![]() 时,求某个时间段需要检查污染源处理系统的概率;
时,求某个时间段需要检查污染源处理系统的概率;
(2)若每套环境监测系统运行成本为300元/小时(不启动则不产生运行费用),除运行费用外,所有的环境监测系统每年的维修和保养费用需要100万元.现以此方案实施,问该企业的环境监测费用是否会超过预算(全年按9000小时计算)?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为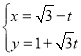 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com