
某糖厂为了了解一条自动生产线上袋装白糖的重量,随机抽取了100袋,并称出每袋白糖的重量(单位:g),得到如下频率分布表。
| 分组 | 频数 | 频率 |
| [485.5,490.5) | 10 |  |
| [490.5,495.5) | 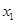 |  |
| [495.5,500.5) | 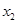 | 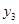 |
| [500.5,505.5] | 10 | |
| 合计 | 100 | |
 ,
, ,
,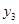 成等差数列。
成等差数列。(1)分组 频数 频率 [485.5,490.5) 10 0.1 [490.5,495.5) 30 0.3 [495.5,500.5) 50 0.5 [500.5,505.5] 10 0.1 合计 100 1 
(2)这100包白糖重量的中位数为496.5g
解析试题分析:(1)根据题意,频率等于频数除以样本容量,那么可知随机抽取了100袋,以每5克为一个组来分为4组来得到频率值0.1,0.3,0.5,0.1,进而得到表格。分组 频数 频率 [485.5,490.5) 10 0.1 [490.5,495.5) 30 0.3 [495.5,500.5) 50 0.5 [500.5,505.5] 10 0.1 合计 100 1 
(2)由频率分布直方图知中位数应在第三组设中位数为
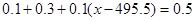
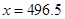
这100包白糖重量的中位数为496.5g
考点:直方图和频率分布表
点评:主要是考查了频率分布表和直方图的运用,属于基础题。


科目:高中数学 来源: 题型:解答题
某校高三4班有50名学生进行了一场投篮测试,其中男生30人,女生20人.为了了解其投篮成绩,甲、乙两人分别都对全班的学生进行编号(1~50号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
| 编号 | 性别 | 投篮成绩 |
| 2 | 男 | 90 |
| 7 | 女 | 60 |
| 12 | 男 | 75 |
| 17 | 男 | 80 |
| 22 | 女 | 83 |
| 27 | 男 | 85 |
| 32 | 女 | 75 |
| 37 | 男 | 80 |
| 42 | 女 | 70 |
| 47 | 女 | 60 |
| 编号 | 性别 | 投篮成绩 |
| 1 | 男 | 95 |
| 8 | 男 | 85 |
| 10 | 男 | 85 |
| 20 | 男 | 70 |
| 23 | 男 | 70 |
| 28 | 男 | 80 |
| 33 | 女 | 60 |
| 35 | 女 | 65 |
| 43 | 女 | 70 |
| 48 | 女 | 60 |
| | 优秀 | 非优秀 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | 10 |
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
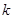 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
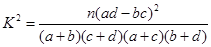 ,其中
,其中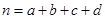 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
7名身高互不相等的学生,分别按下列要求排列,各有多少种不同的排法?
(1)7人站成一排,要求最高的站在中间,并向左、右两边看,身高逐个递减;
(2)任取6名学生,排成二排三列,使每一列的前排学生比后排学生矮.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y (件 ) | 90 | 84 | 83 | 80 | 75 | 68 |
 与单价
与单价 间的回归直线方程;
间的回归直线方程;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出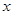 与销售额
与销售额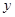 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。
(1)如下的列联表:
| | 男 | 女 | 总计 |
| 爱好 | 40 | | |
| 不爱好 | | 30 | |
| 总计 | | | |
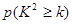 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
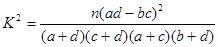
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了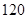 人,其中女性
人,其中女性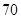 人,男性
人,男性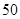 人.女性中有
人.女性中有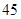 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外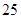 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外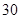 人主要的休闲方式是运动.
人主要的休闲方式是运动.
(1)根据以上数据建立一个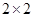 的列联表;
的列联表;
(2)判断性别与休闲方式是否有关系.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表所示:
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学成绩 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理成绩 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
 (1)根据上表完成下面的2×2列联表(单位:人):
(1)根据上表完成下面的2×2列联表(单位:人):| | 数学成绩优秀 | 数学成绩不优秀 | 合 计 |
| 物理成绩优秀 | | | |
| 物理成绩不优秀 | | | |
| 合 计 | | | 20 |
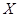 和
和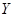 ,它们的值域分别为
,它们的值域分别为 和
和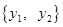 ,其样本频数列联表(称为
,其样本频数列联表(称为 列联表)为:
列联表)为:| | 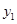 | 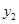 | 合计 |
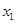 | 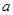 |  | 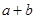 |
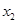 |  | 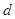 | 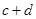 |
| 合计 | 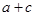 | 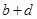 |  |
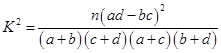 ,其中
,其中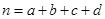 为样本容量;
为样本容量;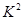 的临界值参考表:
的临界值参考表: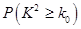 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com