
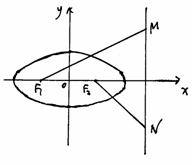
如图,椭圆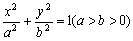 过点P(1,
过点P(1,  ),其左、右焦点分别为F1,F2,离心率e=
),其左、右焦点分别为F1,F2,离心率e=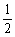 , M, N是直线x=4上的两个动点,且
, M, N是直线x=4上的两个动点,且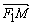 ·
·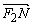 =0.
=0.
(1)求椭圆的方程;
(2)求MN的最小值;
(3)以MN为直径的圆C是否过定点?请证明你的结论。
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
已知直线l1: 4x-3y+6=0和直线l2: x=-1,抛物线y2=4x上一动点P,P到直线l1和直线l2的距离之和的最小值是
A.2 B.3 C.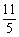 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
设集合A=(―∞, ―2]∪[3, +∞),关于x的不等式(x-2a)·(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p: x∈A, q: x∈B,且Øp是Øq的充分不必要条件,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知双曲线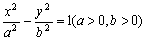 的左焦点为F1,左、右顶点分别为A1、A2,
的左焦点为F1,左、右顶点分别为A1、A2,
P为双曲线上任意一点,则分别以线段PF1,A1A2为直径的两个圆的位置关系为
A.相交 B.相切 C.相离 D.以上情况都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com