
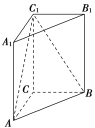
【题目】如图,在直三棱柱ABC![]() 中,AC=3,BC=4,AB=5,A
中,AC=3,BC=4,AB=5,A![]() =4.
=4.
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
【答案】⑴见证明;⑵![]()
【解析】
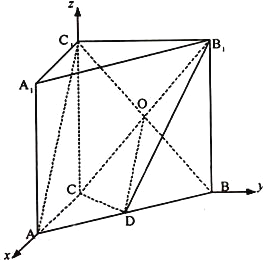
(1)根据AC,BC,CC1两两垂直,建立如图以C为坐标原点,建立空间直角坐标系C﹣xyz,写出要用的点的坐标,根据两个向量的数量级等于0,证出两条线段垂直.
(2)根据所给的两个平面的法向量一个可以直接看出另一个设出根据数量级等于0,求出结果,根据两个平面的法向量所成的角求出两个平面所成的角.
∵直三棱柱ABC﹣A1B1C1,底面三边长AC=3,BC=4,AB=5,
∴AC,BC,CC1两两垂直.
如图以C为坐标原点,建立空间直角坐标系C﹣xyz,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4). …(2分)
证明:(1)∵![]() =(﹣3,0,0),
=(﹣3,0,0),![]() =(0,﹣4,4),
=(0,﹣4,4),
∴![]()
![]() =0,
=0,
故AC⊥BC1…(4分)
解:(2)平面ABC的一个法向量为![]() =(0,0,1),
=(0,0,1),
设平面C1AB的一个法向量为![]() =(x,y,z),
=(x,y,z),
![]() =(﹣3,0,4),
=(﹣3,0,4),![]() =(﹣3,4,0),
=(﹣3,4,0),
由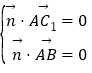 得:
得:![]() …(6分)
…(6分)
令x=4,则z=3,y=3则![]() =(4,3,3).…(7分)
=(4,3,3).…(7分)
故cos<![]() ,
,![]() >=
>=![]() =
=![]() .
.
即二面角![]() ABC的余弦值为
ABC的余弦值为![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ,求点D的坐标;
,求点D的坐标;
(2)问是否存在实数α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,说明理由.
成立?若存在,求出α,β的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )

A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
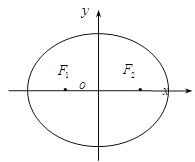
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() (
(![]() ,
,![]() ),且两个焦点
),且两个焦点![]() ,
,![]() 的坐标依次为(
的坐标依次为(![]() 1,0)和(1,0).
1,0)和(1,0).
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求当
,求当![]() 为何值时,直线
为何值时,直线![]() 与以原点为圆心的定圆相切,并写出此定圆的标准方程.
与以原点为圆心的定圆相切,并写出此定圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1 , l2 , 直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16
B.14
C.12
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com