
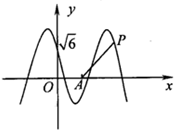
 如图,函数y=2$\sqrt{3}$cos(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的图象与y轴交于点(0,$\sqrt{6}$),周期是π.
如图,函数y=2$\sqrt{3}$cos(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的图象与y轴交于点(0,$\sqrt{6}$),周期是π.分析 (1)由图象与y轴交于点(0,$\sqrt{6}$),周期是π.可得ω和φ的值,从而可得函数解析式,根据余弦函数的性质可求函数图象的对称轴方程和对称中心
(2)点Q(x0,y0)是PA的中点,点A($\frac{π}{2}$,0),利用中点坐标求出P的坐标,点P是该函数图象上一点,代入函数解析式,化简,根据y0=$\frac{\sqrt{6}}{2}$,x0∈[$\frac{π}{2}$,π],求解x0的值.
解答 解:(1)由题意,周期是π,即$ω=\frac{2π}{π}=2$.
由图象与y轴交于点(0,$\sqrt{6}$),∴$\sqrt{6}$=2$\sqrt{3}$cosφ,
可得cosφ=$\frac{\sqrt{2}}{2}$,
∵0≤φ≤$\frac{π}{2}$,
∴φ=$\frac{π}{4}$.
故得函数解析式f(x)=$2\sqrt{3}$cos(2x+$\frac{π}{4}$).
由2x+$\frac{π}{4}$=kπ,可得对称轴方程为:x=$\frac{1}{2}kπ-\frac{π}{8}$,(k∈Z)
由2x+$\frac{π}{4}$=kπ$+\frac{π}{2}$,可得对称中心为($\frac{1}{2}kπ+\frac{π}{8}$,0),(k∈Z)
(2)由题意:点Q(x0,y0)是PA的中点,点A($\frac{π}{2}$,0),
∴P的坐标为($2{x}_{0}-\frac{π}{2}$,2y0),
由y0=$\frac{\sqrt{6}}{2}$,可得:P的坐标为($2{x}_{0}-\frac{π}{2}$,$\sqrt{6}$),
又∵点P是该函数图象上一点,
∴$\sqrt{6}$=2$\sqrt{3}$cos[2×$(2{x}_{0}-\frac{π}{2})+\frac{π}{4}$],
整理可得:cos($4{x}_{0}-\frac{3π}{4}$)=$\frac{\sqrt{2}}{2}$,
∵x0∈[$\frac{π}{2}$,π],
∴$4{x}_{0}-\frac{3π}{4}$∈[$\frac{5π}{4},\frac{13π}{4}$],
故有:$4{x}_{0}-\frac{3π}{4}$=$\frac{7π}{4}$或$4{x}_{0}-\frac{3π}{4}$=$\frac{9π}{4}$,
解得:x0=$\frac{5π}{8}$或${x}_{0}=\frac{3π}{4}$.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )
某几何体的正视图和侧视图如图①,它的俯视图的直观图为矩形O1A1B1C1如图②,其中O1A1=6,O1C1=2,则该几何体的体积为( )| A. | 16$\sqrt{2}$ | B. | 32$\sqrt{2}$ | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com