
分析 由题意画出图形,把求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|的最小值转化为求直角梯形ABCD的中位线长得答案.
解答 解:如图,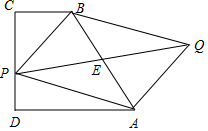
以PA、PB为邻边作平行四边形PAQB,则$\overrightarrow{PA}+\overrightarrow{PB}$=$\overrightarrow{PQ}=2\overrightarrow{PE}$,
要使|$\overrightarrow{PQ}$|取最小值,只需|$\overrightarrow{PE}$|取最小值,
∵E为AB的中点,故当PE⊥CD时,|$\overrightarrow{PE}$|取最小值,
这时PE为梯形的中位线,
即$|\overrightarrow{PE}{|}_{min}=\frac{1}{2}$(|BC|+|AD|)=$\frac{3}{2}$,
故$|\overrightarrow{PQ}{|}_{min}$=3.
故答案为:3.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,是中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 50 | C. | $\frac{99}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
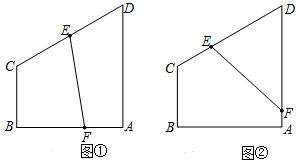
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com