
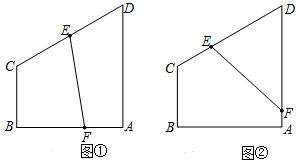
分析 (1)取AB中点G,则四边形BCEF的面积为$\frac{1}{2}{S_{梯形ABCD}}={S_{梯形BCEG}}+{S_{△EFG}}$,求出GF,即可求灌溉水管EF的长度;
(2)△ADC中,由余弦定理,得$EF=\sqrt{{a^2}+{b^2}-ab}≥\sqrt{ab}=\sqrt{3}$,即可求灌溉水管EF的最短长度.
解答 解:(1)因为AD=DC=2,BC=1,∠ABC=∠BAD=90°,
所以$AB=\sqrt{3}$,…(2分)
取AB中点G,则四边形BCEF的面积为$\frac{1}{2}{S_{梯形ABCD}}={S_{梯形BCEG}}+{S_{△EFG}}$,
即$\frac{1}{2}×\frac{1}{2}×\sqrt{3}(1+2)$=$\frac{1}{2}×\frac{{\sqrt{3}}}{2}(1+\frac{3}{2})+\frac{1}{2}GF×\frac{3}{2}$,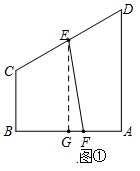
解得$GF=\frac{{\sqrt{3}}}{6}$,…(6分)
所以$EF=\sqrt{{{(\frac{3}{2})}^2}+{{(\frac{{\sqrt{3}}}{6})}^2}}=\frac{{\sqrt{21}}}{3}$(km).
故灌溉水管EF的长度为$\frac{{\sqrt{21}}}{3}$km.…(8分)
(2)设DE=a,DF=b,在△ABC中,$CA=\sqrt{{1^2}+{{(\sqrt{3})}^2}}=2$,
所以在△ADC中,AD=DC=CA=2,
所以∠ADC=60°,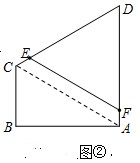
所以△DEF的面积为${S_{△DEF}}=\frac{1}{2}absin60°=\frac{{\sqrt{3}}}{4}ab$,
又${S_{梯形ABCD}}=\frac{{3\sqrt{3}}}{2}$,所以$\frac{{\sqrt{3}}}{4}ab=\frac{{3\sqrt{3}}}{4}$,即ab=3.…(12分)
在△ADC中,由余弦定理,得$EF=\sqrt{{a^2}+{b^2}-ab}≥\sqrt{ab}=\sqrt{3}$,
当且仅当$a=b=\sqrt{3}$时,取“=”.
故灌溉水管EF的最短长度为$\sqrt{3}$km.…(16分)
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,考查余弦定理,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平面直角坐标系xOy中,已知A,B1,B2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右、下、上顶点,F是椭圆C的右焦点.若B2F⊥AB1,则椭圆C的离心率是$\frac{\sqrt{5}-1}{2}$.
如图,在平面直角坐标系xOy中,已知A,B1,B2分别为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右、下、上顶点,F是椭圆C的右焦点.若B2F⊥AB1,则椭圆C的离心率是$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区.
如图所示,有一块矩形空地ABCD,AB=2km,BC=4km,根据周边环境及地形实际,当地政府规划在该空地内建一个筝形商业区AEFG,筝形的顶点A,E,F,G为商业区的四个入口,其中入口F在边BC上(不包含顶点),入口E,G分别在边AB,AD上,且满足点A,F恰好关于直线EG对称,矩形内筝形外的区域均为绿化区.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,40] | B. | [160,+∞) | C. | (-∞,40)∪(160,+∞) | D. | (-∞,40]∪[160,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com