
分析 由题意,只要证明数列an=${2}^{{2}^{n}}$+1(n=0,1,2,….)的任意相邻两项都是互素的.利用反证法证明即可.
解答 证明:由题意,只要证明数列an=${2}^{{2}^{n}}$+1(n=0,1,2,….)的任意相邻两项都是互素的.
假设an+1与an不是互素的,则存在t=$\frac{{a}_{n+1}}{{a}_{n}}$≥2,t∈N+,
∴t-1=$\frac{{2}^{{2}^{n}}({2}^{{2}^{n}}-1)}{{2}^{{2}^{n}}+1}$≥1,t∈N+,
设m=${2}^{{2}^{n}}$+1,则t-1=$\frac{(m-1)(m-2)}{m}$=m-3+$\frac{2}{m}$,
∵m≥3,m∈N+,
∴m-3+$\frac{2}{m}$∉N+,
与t-1∈N+矛盾,
∴an+1与an不是互素的不成立,
∴数列an=${2}^{{2}^{n}}$+1(n=0,1,2,….)的任意两项都是互素的.
点评 本题考查数列知识,考查用反证法证明数学命题,推出矛盾,是解题的关键和难点,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (0,+∞) | C. | [-2,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{3\sqrt{5}}}{2},+∞)$ | B. | $(1,\frac{3}{2}]$ | C. | $(1,\frac{{3\sqrt{5}}}{2}]$ | D. | $[\frac{3}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
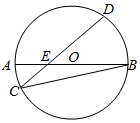 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )| A. | 1 | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{7}}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
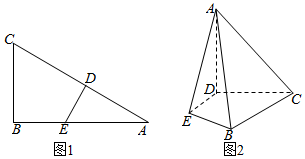 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com