Question

已知直线l1：x－2y－1＝0，直线l2：ax－by＋1＝0，其中a，b∈{1，2，3，4，5，6}．

(1) 求直线l1∩l2＝?的概率；

(2) 求直线l1与l2的交点位于第一象限的概率．

 

Answer 1

(1) (2)

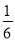
【解析】(1) 直线l1的斜率k1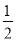＝，直线l2的斜率k2＝.设事件A为“直线l1∩l2＝?”．a，b∈{1，2，3，4，5，6}的总事件数为(1，1)，(1，2)，…，(1，6)，(2，1)，(2，2)，…，(2，6)，…，(5，6)，(6，6)共36种．若l1∩l2＝?，则l1∥l2，即k1＝k2，即b＝2a.满足条件的实数对(a，b)有(1，2)，(2，4)，(3，6)共三种情况．所以P(A)＝.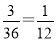

(2) 设事件B为“直线l1与l2的交点位于第一象限”，由于直线l1与l2有交点，则b≠2a.联立方程组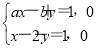解得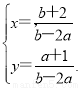 ∵ l1与l2的交点位于第一象限，∴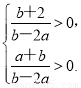

∵ a、b∈{1，2，3，4，5，6}，∴ b>2a.∴ 总事件数共36种，满足b>2a的事件有(1，3)，(1，4)，(1，5)，(1，6)，(2，5)，(2，6)，共6种，∴ P(B)＝