练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    “抛阶砖”是国外游乐场的典型游戏之一．参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上，抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠)，便可获大奖.不少人被高额奖金所吸引，纷纷参与此游戏但很少有人得到奖品，请用所学的概率知识解释这是为什么．

     

     

    0.0022.

    【解析】在抛阶砖游戏中，首先可以判定此试验为几何概型，我们为了描述每一次随机试验的结果只需要确定金币圆心O的位置即可，一旦圆心位置确定，只要当圆心O到其最近正方形的各边的距离大于其半径时，便可获大奖．由此不难想到一种临界状态，就是当金币与正方形的一边相切时，此时圆心O到该边的距离为1，显然只有当圆心O到最近正方形的各边的距离大于1时才能获奖，所以若中奖，金币圆心必位于小正方形区域A内．若中奖，金币圆心必位于下图的小正方形区域A内．圆心随机地落在“阶砖”的任何位置，所以这是一个几何概型．其概率为≈0.0022.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－2第2课时练习卷（解析版） 题型：解答题

    矩阵M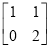＝有特征向量为e1＝，e2＝，

    (1)求e1和e2对应的特征值；

    (2)对向量α＝，记作α＝e1＋3e2，利用这一表达式间接计算M4α，M10α.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第2课时练习卷（解析版） 题型：解答题

    如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.

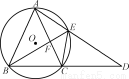
    (1)判断BE是否平分∠ABC，并说明理由；

    (2)若AE＝6，BE＝8，求EF的长．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第1课时练习卷（解析版） 题型：解答题

    如图，在梯形ABCD中，AD∥BC，AC⊥BD，垂足为E，∠ABC＝45°，过E作AD的垂线交AD于F，交BC于G，过E作AD的平行线交AB于H.求证：FG2＝AF·DF＋BG·CG＋AH·BH.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨选修4－1第1课时练习卷（解析版） 题型：解答题

    如图，四边形ABCD中，DF⊥AB，垂足为F，DF＝3，AF＝2FB＝2，延长FB到E，使BE＝FB.连结BD、EC，若BD∥EC，求△BCD和四边形ABCD的面积．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十章第6课时练习卷（解析版） 题型：填空题

    在一个盒子中有分别标有数字1，2，3，4，5的5张卡片，现从中一次取出2张卡片，则取到的卡片上的数字之积为偶数的概率是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十章第6课时练习卷（解析版） 题型：解答题

    如图，∠AOB＝60°，OA＝2，OB＝5，在线段OB上任取一点C，试求：

    (1)△AOC为钝角三角形的概率；

    (2)△AOC为锐角三角形的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十章第5课时练习卷（解析版） 题型：解答题

    已知直线l1：x－2y－1＝0，直线l2：ax－by＋1＝0，其中a，b∈{1，2，3，4，5，6}．

    (1) 求直线l1∩l2＝?的概率；

    (2) 求直线l1与l2的交点位于第一象限的概率．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第十章第3课时练习卷（解析版） 题型：填空题

    某射击选手连续射击5枪命中的环数分别为：9.7，9.9，10.1，10.2，10.1，则这组数据的方差为________．

     

    查看答案和解析>>

    同步练习册答案