
| A. | 8π | B. | 16π | C. | $\frac{16}{3}π$ | D. | $\frac{32}{3}π$ |
分析 求出棱锥的最大高度,利用勾股定理计算外接圆的半径,从而得出球的体积.
解答 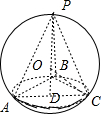 解:∵△ABC是等腰直角三角形,
解:∵△ABC是等腰直角三角形,
∴AC为截面圆的直径,故外接球的球心O在截面ABC中的射影为AC的中点D,
∴当P,O,D共线且P,O位于截面同一侧时棱锥的体积最大,
棱锥的最大高度为PD,
∴$\frac{1}{3}$×$\frac{1}{2}$×$\sqrt{6}$×$\sqrt{6}$×PD=3,解得PD=3,
设外接球的半径为R,则OD=3-R,OC=R,
在△ODC中,CD=$\frac{1}{2}$AC=$\sqrt{3}$,
由勾股定理得:(3-R)2+3=R2,解得R=2.
∴外接球的体积V=$\frac{4π}{3}$×23=$\frac{32π}{3}$.
故选:D.
点评 本题考查了棱锥与球的位置关系,几何体的体积计算,属于中档题.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
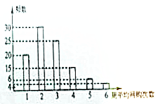 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.40 | C. | 0.64 | D. | 0.75 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn=2Tn | B. | Tn=2bn+1 | C. | Tn>an | D. | Tn<bn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
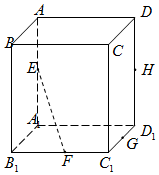 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则下列直线中与直线EF相交的是( )| A. | 直线CC1 | B. | 直线C1D1 | C. | 直线HC1 | D. | 直线GH |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com