
 如图,已知ABCD为平行四边形,∠A=60°,线段AB上点F满足AF=2FB,AB长为12,点E在CD上,EF∥BC,BD⊥AD,BD与EF相交于N.现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上.
如图,已知ABCD为平行四边形,∠A=60°,线段AB上点F满足AF=2FB,AB长为12,点E在CD上,EF∥BC,BD⊥AD,BD与EF相交于N.现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上.分析 (Ⅰ)先证明出EF⊥平面BDN,根据面面垂直的判定定理证明出平面BDN⊥平面BCEF,根据BN为平面BDN与平面BCEF的交线,进而推断D在平面BCEF上的射影在直线BN上
,进而推断D在平面BCEF上的射影即为点B,证明出结论.
(Ⅱ)DB⊥底面BCEF,所以∠DEB为DE与平面BCEF所成的角.
解答 (Ⅰ)证明:EF⊥DN,EF⊥BN,
∴EF⊥平面BDN,
∴平面BDN⊥平面BCEF,
又∵BN为平面BDN与平面BCEF的交线,
∴D在平面BCEF上的射影在直线BN上,
而D在平面BCEF上的射影在BC上,
∴D在平面BCEF上的射影即为点B,
即BD⊥平面BCEF.
(Ⅱ)解:如图,D在平面BCEF上的射影点为点B,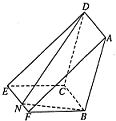
∴∠DEB为DE与平面BCEF所成的角,
DE=AF=8,NF=2,NE=4,NB=2$\sqrt{3}$,NB⊥NE,
∴BE=2$\sqrt{7}$,DB=$\sqrt{D{E}^{2}-B{E}^{2}}$=6,
∴sin∠DEB=$\frac{DB}{DE}$=$\frac{3}{4}$,
即直线DE与平面BCEF所成角的正弦值为$\frac{3}{4}$.
点评 本题主要考查了线面垂直,线面平行判定定理及其性质的运用,平面法向量的运用.综合考查了学生分析能力和解题能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {(4,0),(0,2)} | C. | {4,2} | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{1}{2}$i | B. | -$\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.
已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
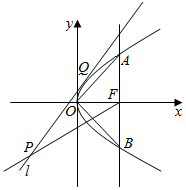 已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com