
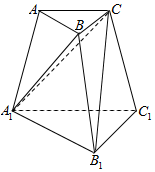
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$. 分析 假设△AnBnCn的面积为Sn,OAn与平面AnBnCn所成的角为α,利用相似三角形得出$\frac{{S}_{1}}{{S}_{n}}$=($\frac{{a}_{1}}{{a}_{n}}$)2=$\frac{2}{{{a}_{n}}^{2}}$,用S1,α表示出V${\;}_{O-{A}_{1}{B}_{1}{C}_{1}}$和每个小三棱台的体积V台,根据V${\;}_{O-{A}_{n}{B}_{n}{C}_{n}}$=$\frac{1}{3}{S}_{n}{a}_{n}sinα$=(n-1)V台+V${\;}_{O-{A}_{1}{B}_{1}{C}_{1}}$列出方程解出an.
解答 解:设△AnBnCn的面积为Sn,OAn与平面AnBnCn所成的角为α,则棱锥O-AnBnCn的高为ansinα.
∵△A1B1C1∽△A1BnCn,
∴$\frac{{S}_{1}}{{S}_{n}}$=($\frac{{A}_{1}{C}_{1}}{{A}_{n}{C}_{n}}$)2,
∵△OA1C1∽△OAnCn,
∴$\frac{{A}_{1}{C}_{1}}{{A}_{n}{C}_{n}}$=$\frac{O{A}_{1}}{O{A}_{n}}$=$\frac{{a}_{1}}{{a}_{n}}$.
∴$\frac{{S}_{1}}{{S}_{n}}$=($\frac{{a}_{1}}{{a}_{n}}$)2=$\frac{2}{{{a}_{n}}^{2}}$,
∴Sn=$\frac{{{a}_{n}}^{2}•{S}_{1}}{2}$.
∴V${\;}_{O-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}{S}_{1}{a}_{1}sinα$=$\frac{\sqrt{2}}{3}$S1sinα,V${\;}_{O-{A}_{2}{B}_{2}{C}_{2}}$=$\frac{1}{3}{S}_{2}{a}_{2}sinα$=$\frac{4}{3}{S}_{1}sinα$,
∴每个小三棱台的体积V台=V${\;}_{O-{A}_{2}{B}_{2}{C}_{2}}$-V${\;}_{O-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{4-\sqrt{2}}{3}{S}_{1}sinα$.
∴V${\;}_{O-{A}_{n}{B}_{n}{C}_{n}}$=$\frac{1}{3}{S}_{n}{a}_{n}sinα$=(n-1)V台+V${\;}_{O-{A}_{1}{B}_{1}{C}_{1}}$.
∴$\frac{1}{3}•$$\frac{{{a}_{n}}^{2}•{S}_{1}}{2}$•ansinα=(n-1)•$\frac{4-\sqrt{2}}{3}{S}_{1}sinα$+$\frac{\sqrt{2}}{3}$S1sinα.
∴an3=2(n-1)$•(4-\sqrt{2})$+2$\sqrt{2}$=8n-2$\sqrt{2}$n-8+4$\sqrt{2}$.
∴an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
故答案为:an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$
点评 本题考查了棱台,棱锥的体积计算,公式推导较复杂,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+(y+2)2=9 | B. | (x+1)2+(y-2)2=9 | C. | (x-1)2+(y-2)2=9 | D. | (x-1)2+(y+2)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知ABCD为平行四边形,∠A=60°,线段AB上点F满足AF=2FB,AB长为12,点E在CD上,EF∥BC,BD⊥AD,BD与EF相交于N.现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上.
如图,已知ABCD为平行四边形,∠A=60°,线段AB上点F满足AF=2FB,AB长为12,点E在CD上,EF∥BC,BD⊥AD,BD与EF相交于N.现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1:\sqrt{3}$ | B. | 1:3 | C. | $1:3\sqrt{3}$ | D. | 1:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:4 | B. | 1:5 | C. | 1:6 | D. | 1:7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com