
分析 (I)通过x≥1与0<x<1,化简函数的表达式,求出函数的导数,判断导数的符号,推出函数的单调性.
(II)利用x≥1,转化f(x)≥a(x-1)为(x+1)lnx-a(x-1)≥0,构造函数g(x)=(x+1)lnx-a(x-1),求出函数的导数,利用(I)的结果,推出a的范围.
解答 解:(I)当$x≥1,f(x)=({x+1})lnx,f′(x)=1+\frac{1}{x}+lnx>0$,
f(x)在(1,+∞)上递增;------------------------(3分)
$0<x<1,f(x)=-({x+1})lnx,f′(x)=-({1+\frac{1}{x}+lnx})$,$f′′(x)=-({\frac{1}{x}-\frac{1}{x^2}})=\frac{1-x}{x^2}>0$,
f′(x)在(0,1)递增,f′(x)<f′(1)=-2<0,f(x)在(0,1)上递减
所以f(x)在(0,1)上递减,在(1,+∞)上递增.------------------------(6分)
(II)x≥1,f(x)=(x+1)lnx,f(x)≥a(x-1)?(x+1)lnx-a(x-1)≥0
设$g(x)=({x+1})lnx-a({x-1}),g′(x)=1+\frac{1}{x}+lnx-a$
由(I)知,g′(x)在(1,+∞)上递增,g′(x)≥g′(1)=2-a
若2-a≥0,即a≤2,g′(x)≥0,g(x)在[1,+∞)上递增,
∴g(x)≥g(1)=0,所以不等式成立---------------------------(9分)
若a>2,存在x0∈(1,+∞),使得g′(x0)=0,当x∈[1,x0)时,g′(x)<0,g(x)是减函数,
∴g(x)<g(1)=0,这与题设矛盾------------(12分)
综上所述,a≤2.
点评 本题考查函数的导数的综合应用,函数的单调性的判断,构造法二次求导,考查转化思想以及分类讨论思想的应用,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
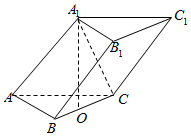 如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.
如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com