
| A. | $1:\sqrt{3}$ | B. | 1:3 | C. | $1:3\sqrt{3}$ | D. | 1:9 |
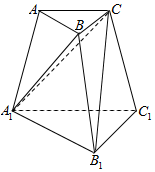
分析 把C当做棱锥的顶点,则两棱锥的高相等,故体积比为底面积之比,而两底面三角形的高又相等,故体积比为AB:A1B1=1:3.
解答 解:设C到平面AA1B1B的距离为h,
∵AB:A1B1=1:3,
∴S${\;}_{△{A}_{1}AB}$:S${\;}_{△{A}_{1}{B}_{1}B}$=1:3.
∵V${\;}_{{A}_{1}-ABC}$=V${\;}_{C-{A}_{1}AB}$=$\frac{1}{3}{S}_{△{A}_{1}AB}$•h.
V${\;}_{B-{A}_{1}{B}_{1}C}$=V${\;}_{C-{A}_{1}{B}_{1}B}$=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}B}•h$.
∴V${\;}_{{A}_{1}-ABC}$:V${\;}_{B-{A}_{1}{B}_{1}C}$=S${\;}_{△{A}_{1}AB}$:S${\;}_{△{A}_{1}{B}_{1}B}$=1:3.
故选B.
点评 本题考查了棱锥的体积公式,属于基础题.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (3,4] | C. | (-∞,3)∪[4,+∞) | D. | (-∞,-1)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{1}{2}$i | B. | -$\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.
已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
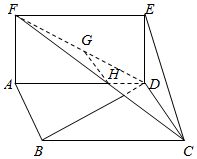 如图,平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面和平面ABCD垂直,G,H分别是DF,FC的中点.
如图,平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面和平面ABCD垂直,G,H分别是DF,FC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com