
| A. | 1:4 | B. | 1:5 | C. | 1:6 | D. | 1:7 |
分析 利用三角形面积公式,可把△BCF与△ACF的面积之比转化为BC长与AC长的比,再根据抛物线的焦半径公式借助|BF|=$\frac{3}{2}$求出B点坐标,得到AB方程,代入抛物线方程,解出A点坐标,就可求出BC与AC的长度之比,得到所需问题的解.
解答  解:∵抛物线方程y2=4x的焦点为F坐标为(1,0),准线方程为x=-1
解:∵抛物线方程y2=4x的焦点为F坐标为(1,0),准线方程为x=-1
设A(x1,y1),B(x2,y2),则|BF|=x2+1=$\frac{3}{2}$,
∴x2=$\frac{1}{2}$
把x2=$\frac{1}{2}$代入抛物线y2=4x得y=±$\sqrt{2}$,不妨取y2=-$\sqrt{2}$,即B($\frac{1}{2}$,-$\sqrt{2}$)为例进行研究
∴直线AB过点M(2,0)与B($\frac{1}{2}$,-$\sqrt{2}$)
方程为y=$\frac{2\sqrt{2}}{3}$(x-2),代入抛物线方程,解得,x1=8,
∴|AE|=8+1=9,
∵在△AEC中,BN∥AE,
∴△BCF与△ACF的面积的比值为=$\frac{|BC|}{|AC|}$=$\frac{|BN|}{|AE|}$=$\frac{\frac{3}{2}}{9}$=$\frac{1}{6}$,
故选:C.
点评 本题主要考查了抛物线的焦半径公式,侧重了学生的转化能力,以及计算能力.


科目:高中数学 来源: 题型:填空题
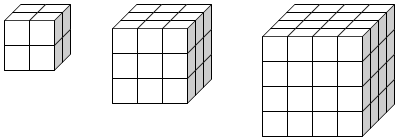
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
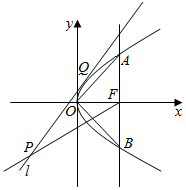 已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com