
分析 设a=$\frac{9{x}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,b=$\frac{9{y}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,c=$\frac{9{z}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,x+y+z=1,则原不等式即为x2+y2+z2≥9(x2y2+y2z2+z2x2),不妨设x≥y≥z,则$\frac{1}{3\sqrt{3}}$≤z≤$\frac{1}{3}$,令f(x,y,z)=x2+y2+z2-9(x2y2+y2z2+z2x2),证明大于等于0,运用分析法,即可得证.
解答 证明:设a=$\frac{9{x}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,b=$\frac{9{y}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,c=$\frac{9{z}^{2}}{{x}^{2}+{y}^{2}+{z}^{2}}$,x+y+z=1,
则原不等式即为x2+y2+z2≥9(x2y2+y2z2+z2x2),
由a≥1,9x2=a(x2+y2+z2)≥x2+y2+z2≥$\frac{(x+y+z)^{2}}{3}$=$\frac{1}{3}$,
即有x≥$\frac{1}{3\sqrt{3}}$,同理y≥$\frac{1}{3\sqrt{3}}$,z≥$\frac{1}{3\sqrt{3}}$,
不妨设x≥y≥z,则$\frac{1}{3\sqrt{3}}$≤z≤$\frac{1}{3}$,
$\frac{1}{3}$≤$\frac{x+y}{2}$=$\frac{1-z}{2}$≤$\frac{3\sqrt{3}-1}{6\sqrt{3}}$,
令f(x,y,z)=x2+y2+z2-9(x2y2+y2z2+z2x2),
则f(x,y,z)-f($\frac{x+y}{2}$,$\frac{x+y}{2}$,z)=$\frac{(x-y)^{2}}{2}$[1-9z2+$\frac{9}{8}$(x+y)2+$\frac{9}{2}$xy]≥0,
只需证t∈[$\frac{1}{3}$,$\frac{3\sqrt{3}-1}{6\sqrt{3}}$],f(t,t,1-2t)≥0.
而f(t,t,1-2t)=2t2+(1-2t)2-9[t4+2t2(1-2t)2]
=(3t-1)2(1+2t-9t2)≥0?$\frac{1-\sqrt{10}}{9}$≤t≤$\frac{1+\sqrt{10}}{9}$.
故只需验证$\frac{3\sqrt{3}-1}{6\sqrt{3}}$<$\frac{1+\sqrt{10}}{9}$.显然成立.
则原不等式成立.
点评 本题考查不等式的证明,注意运用换元法和柯西不等式,以及构造函数法,不等式的性质,考查推理和运算能力,属于难题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {(4,0),(0,2)} | C. | {4,2} | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.
如图,互不相同的点A1、A2、…An、…,Bi、B2、…Bn、…,Cl、C2、…Cn、…分别在以O为顶点的三棱锥的三条侧棱上,所有平面AnBnCn互相平行,且所有三棱台AnBnCn-An+1Bn+1Cn+1的体积均相等,设OAn=an,若a1=$\sqrt{2}$,a2=2,则an=$\root{3}{8n-2\sqrt{2}n-8+4\sqrt{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
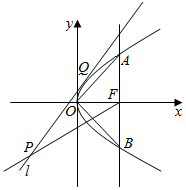 已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com