练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若a∈R，解关于x的不等式
    2-x
    a+x
    ＜1．
    考点：一元二次不等式的解法
    专题：不等式的解法及应用
    分析：原不等式可化为(x+a)(x-1+
    a
    2
    )＞0    ．通过对a分类讨论，再利用一元二次不等式的解法即可得出．
    解答： 解：原不等式可化为(x+a)(x-1+
    a
    2
    )＞0    ．
    （1）当a=-2时，解集为：{x|x≠2}；
    （2）当a＞-2时，解集为：{x|x＞1-
    a
    2
    或x＜-a}；
    （3）当a＜-2时，解集为：{x|x＞-a或x＜1-
    a
    2
    }．
    点评：本题考查了分式不等式转化为一元二次不等式的解法，考查了分类讨论的思想方法，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=|2x-1|+|2x+a|，g（x）=x+3．
    （Ⅰ）当a=-2时，求不等式f（x）＜g（x）的解集；
    （Ⅱ）当x∈（
    1
    2
    ，1）时，f（x）≤g（x）成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于D．E，F分别为弦AB与弦AC上的点，B，E，F，C四点共圆，且BC•AE=DC•AF．
    （1）证明：CA是△ABC外接圆的直径；
    （2）若DB=BE=EA，求过B，E，F，C四点的圆的半径与△ABC外接圆半径的比值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的一个顶点与抛物线x2=4
    		2
    y的焦点重合，F1，F2分布是椭圆的左、右焦点，离心率e=
    		3
    3
    ，过椭圆右焦点F2的直线l与椭圆C交于M，N两点，O为坐标原点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）当
    OM
    •
    ON
    =-1时，求直线l的方程；
    （Ⅲ）若AB是椭圆C经过原点O的弦，MN∥AB，是否存在常数λ，使|AB|=λ
    		|MN|
    ？若存在，求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=asinx+cosx，a∈R；
    （Ⅰ）求在点（
    π
    2
    ，1）的切线方程；
    （Ⅱ）若a=f′（
    π
    2
    ），求f（
    π
    4
    ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设A={（x，y）|y2=x+1}，B={（x，y）|y=2x2+x+
    5
    2
    }，C={（x，y）|y=kx+b}，是否存在k，b∈N*，使（A∪B）∩C=∅，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}的前n项和为Sn，满足Sn=an+1-2n+1+1，（n∈N*），且a1=1．
    （1）求数列{an}的通项公式；
    （2）设数列{bn}满足bn=
    an+1-1
    an+1+2
    ，数列{bn}的前n项和为Tn，证明：对一切正整数n，都有n-
    3
    2
    ＜Tn＜n-
    1
    4
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

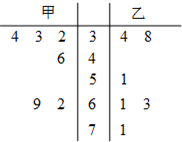    近年来，我国许多地方出现雾霾天气，影响了人们的出行、工作与健康．其形成与 PM2.5有关．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．PM2.5日均值越小，空气质量越好．为加强生态文明建设，我国国家环保部于2012年2月29日，发布了《环境空气质量标准》见下表：
    PM2.5日均值k（微克）空气质量等级
    k≤35一级
    35＜k≤75二级
    k＞75超标
    某环保部门为了了解甲、乙两市的空气质量状况，在某月中分别随机抽取了甲、乙两市6天的 PM2.5日均值作为样本，样本数据茎叶图如图所示（十位为茎，个位为叶）．
    （Ⅰ）求甲、乙两市PM2.5日均值的样本平均数，据此判断该月中哪个市的空气质量较好；
    （Ⅱ）若从甲市这6天的样本数据中随机抽取两天的数据，求恰有一天空气质量等级为一级的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在平行四边形ABCD中，AP⊥BD，垂足为P，AP=3，点Q是△BCD内（包括边界）的动点，则
    AP
    •
    AQ
    的取值范围是
     
    ．

    查看答案和解析>>

    同步练习册答案