
���� ��I��ͨ����${a_{n+1}}=\frac{{2{a_n}}}{{1+{a_n}}}��n��{N^*}$ȡ���������ο�֪an��0��$\frac{1}{{a}_{n+1}}$-1=$\frac{1}{2}$��$\frac{1}{{a}_{n}}$-1����������֪����{$\frac{1}{{a}_{n}}$-1}������Ϊ1������Ϊ$\frac{1}{2}$�ĵȱ����У����õȱ�����ͨ�ʽ���㼴�ý��ۣ�
��II��ͨ����I����֪bn=n+n•$\frac{1}{{2}^{n-1}}$���������÷�����ͷ�����λ����������֪Sn=$\frac{{n}^{2}}{2}$+4+$\frac{n•{2}^{n-1}-2n-4}{{2}^{n}}$����n��3ʱ�������ý��ۣ�
��� ֤������I��������֪an��0��$\frac{1}{{a}_{n+1}}$-1=$\frac{1+{a}_{n}}{2{a}_{n}}$-1=$\frac{1}{2}$��$\frac{1}{{a}_{n}}$-1����
����Ϊ$\frac{1}{{a}_{1}}$-1=1��
��������{$\frac{1}{{a}_{n}}$-1}������Ϊ1������Ϊ$\frac{1}{2}$�ĵȱ����У�
����$\frac{1}{{a}_{n}}$-1=$\frac{1}{{2}^{n-1}}$����$\frac{1}{{a}_{n}}$=1+$\frac{1}{{2}^{n-1}}$��an=$\frac{{2}^{n-1}}{1+{2}^{n-1}}$��
��II���ɣ�I����֪bn=n+n•$\frac{1}{{2}^{n-1}}$��
��Sn=��1+2+3+��+n��+��1•$\frac{1}{{2}^{0}}$+2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+��+n•$\frac{1}{{2}^{n-1}}$��
=$\frac{n��n+1��}{2}$+��1•$\frac{1}{{2}^{0}}$+2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+��+n•$\frac{1}{{2}^{n-1}}$����
$\frac{1}{2}$Sn=$\frac{n��n+1��}{4}$+[1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+��+��n-1��•$\frac{1}{{2}^{n-1}}$+n•$\frac{1}{{2}^{n}}$]��
��ʽ������ã�$\frac{1}{2}$Sn=$\frac{n��n+1��}{4}$+��$\frac{1}{{2}^{0}}$+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$��
=$\frac{n��n+1��}{4}$+$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$
=$\frac{n��n+1��}{4}$+2-$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$��
����Sn=$\frac{{n}^{2}}{2}$+4+$\frac{n•{2}^{n-1}-2n-4}{{2}^{n}}$��
��n��3ʱ��n•2n-1-2n-4��n•22-2n-4��0��
����Sn��$\frac{{n}^{2}}{2}$+4��
���� ������һ�����������벻��ʽ���ۺ��⣬�������е�ͨ�ǰn��ͣ������λ������������������������ע����ⷽ���Ļ��ۣ������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
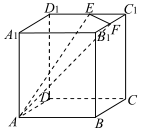 ��ͼ��ʾ�����ⳤΪ 6��������ABCD-A1B1C1D1�У���E��F�ֱ�����C1D1��B1C1���е㣬��A��E��F��������������Ľ��棬�������ܳ�Ϊ��������
��ͼ��ʾ�����ⳤΪ 6��������ABCD-A1B1C1D1�У���E��F�ֱ�����C1D1��B1C1���е㣬��A��E��F��������������Ľ��棬�������ܳ�Ϊ��������| A�� | $18+3\sqrt{2}$ | B�� | $6\sqrt{13}+3\sqrt{2}$ | C�� | $6\sqrt{5}+9\sqrt{2}$ | D�� | $10+3\sqrt{2}+4\sqrt{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45�� | B�� | 120�� | C�� | 60�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
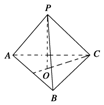 ��֪��P����������ABC����ƽ����һ�㣬PA=PB=PC=$\frac{2}{3}$��AB=1����PC��ƽ��ABC���ɵĽ��ǣ�������
��֪��P����������ABC����ƽ����һ�㣬PA=PB=PC=$\frac{2}{3}$��AB=1����PC��ƽ��ABC���ɵĽ��ǣ�������| A�� | 90�� | B�� | 60�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{25}{8}$ | B�� | $\frac{25}{4}$ | C�� | 25 | D�� | $\frac{4}{25}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com