Question

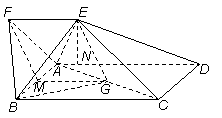
如图，四边形ABCD为矩形，四边形ADEF为梯形，AD//FE，∠AFE=60º，且平面ABCD⊥平面ADEF，AF=FE=AB=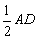=2，点G为AC的中点．

（Ⅰ）求证：EG//平面ABF；

（Ⅱ）求三棱锥B-AEG的体积；

（Ⅲ）试判断平面BAE与平面DCE是否垂直？若垂直，请证明；若不垂直，请说明理由．

Answer 1

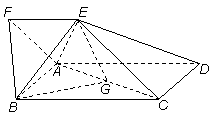
（I）证明：取AB中点M，连FM，GM．

∵ G为对角线AC的中点，

∴ GM∥AD，且GM=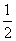AD，

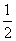又∵ FE∥AD，

∴ GM∥FE且GM=FE．

∴四边形GMFE为平行四边形，即EG∥FM．

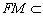又∵ 平面ABF，平面ABF，

∴ EG∥平面ABF．

（Ⅱ）解：作EN⊥AD，垂足为N，

由平面ABCD⊥平面AFED ，面ABCD∩面AFED=AD，

得EN⊥平面ABCD，即EN为三棱锥E-ABG的高．

∵ 在△AEF中，AF=FE，∠AFE=60º，

∴ △AEF是正三角形．

∴ ∠AEF=60º，

由EF//AD知∠EAD=60º，

∴ EN=AE∙sin60º=．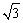

∴ 三棱锥B-AEG的体积为

．

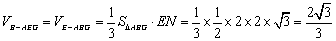（Ⅲ）解：平面BAE⊥平面DCE．证明如下：

∵ 四边形ABCD为矩形，且平面ABCD⊥平面AFED，

∴ CD⊥平面AFED，

∴ CD⊥AE．

∵ 四边形AFED为梯形，FE∥AD，且，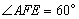

∴ ．

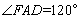又在△AED中，EA=2，AD=4，，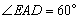

由余弦定理，得ED=．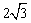

∴ EA²+ED²=AD²，

∴ ED⊥AE．

又∵ ED∩CD=D，

∴ AE⊥平面DCE，

又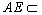面BAE，

∴ 平面BAE⊥平面DCE．