练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
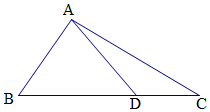
    9．如图，在ABC中，D是BC上的一点．已知∠B=60°，AD=2，AC=$\sqrt{10}$，DC=2，则AB=$\sqrt{5}$．

    分析 利用余弦定理求出cos∠ADC=$\frac{4+4-10}{2×2×2}$=-$\frac{1}{4}$，再利用正弦定理，即可求出AB．

    解答 解：由题意，cos∠ADC=$\frac{4+4-10}{2×2×2}$=-$\frac{1}{4}$，
    ∴cos∠ADB=$\frac{1}{4}$，sin∠ADB=$\frac{\sqrt{15}}{4}$
    ∵∠B=60°，AD=2，
    ∴$\frac{2}{\frac{\sqrt{3}}{2}}=\frac{AB}{\frac{\sqrt{15}}{4}}$，
    ∴AB=$\sqrt{5}$，
    故答案为：$\sqrt{5}$．

    点评 本题考查正弦定理、余弦定理的运用，考查学生的计算能力，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．关于f（x）=3sin（2x+$\frac{π}{4}$）有以下命题，
    ①若f（x1）=f（x2）=0，则x1-x2=kπ（k∈Z）；
    ②f（x）图象与g（x）=3cos（2x-$\frac{π}{4}$）图象相同；
    ③f（x）在区间[-$\frac{7π}{8}$，-$\frac{3π}{8}$]是减函数；
    ④f（x）图象关于点（-$\frac{π}{8}$，0）对称．
    其中正确的命题序号是（　　）
    A．②③④B．①④C．①②③D．②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知矩形ABCD的边AB=4，AD=1，点P为边AB上的一动点，则当∠DPC最大时，线段AP的长为（　　）
    A．1或3B．1.5或2.5C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．关于x的不等式|x+cos2θ|≤sin2θ的解是（　　）
    A．cos2θ≤x≤1B．-1≤x≤-cos2θC．-cos2θ≤x≤1D．-1≤x≤cos2θ

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知点A（-2，-1），B（1，-5），点P是圆C：（x-2）2+（y-1）2=4上的动点，则△PAB面积的最大值与最小值之差为10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．有下列五个命题：
    ①函数y=4cos2x，x∈[-10π，10π]不是周期函数；
    ②已知定义域为R的奇函数f（x），满足f（x+3）=f（x），当x∈（0，$\frac{3}{2}$）时，f（x）=sinπx，则函数f（x）在区间[0，6]上的零点个数是9；
    ③为了得到函数y=-cos2x的图象，可以将函数y=sin（2x-$\frac{π}{6}$）的图象向左平移$\frac{π}{6}$；
    ④已知函数f（x）=x-sinx，若x1，x2∈[-$\frac{π}{2}$，$\frac{π}{2}}$]且f（x1）+f（x2）＞0，则x1+x2＞0；
    ⑤设曲线f（x）=acosx+bsinx的一条对称轴为x=$\frac{π}{5}$，则点（$\frac{2π}{5}$，0）为曲线y=f（$\frac{π}{10}$-x）的一个对称中心．
    其中正确命题的序号是①②④⑤．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{2}$=1的一条渐近线过点（$\sqrt{2}$，1），则此双曲线的一个焦点坐标是（　　）
    A．（$\sqrt{2}，0$）B．（2，0）C．（$\sqrt{6}，0$）D．（$\sqrt{10}，0$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

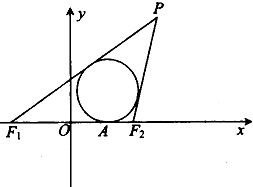    5．在平面直角坐标系中，已知△PF1F2的两个顶点为F1（-$\sqrt{2}$a，0），F2（$\sqrt{2}$a，0）（a＞0），顶点P在曲线C上运动，△PF1F2的内切圆与x轴的切点为A，满足|AF1|-|AF2|=2a．
    （1）设D（m，n）为曲线C上一点，试判断直线l：mx-ny=a2与曲线C的位置关系；
    （2）过曲线C上任意两个不同点M，N分作C的切线l1，l2，若l1与l2的交点为E，试探究：对于任意的正实数a，直线OE（O是原点）是否经过MN的中点G？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30min抽取一包产品，称其重量，分别记录抽查数据如下：
    甲：102，101，99，98，103，98，99；
    乙：110，115，90，85，75，115，110．
    （1）这种抽样方法是哪一种？
    （2）将这两组数据用茎叶图表示；
    （3）将两组数据比较，说明哪个车间的产品较稳定．

    查看答案和解析>>

    同步练习册答案