
分析 (1)当Q为椭圆短轴顶点时,△QF1F2面积最大,列出方程组解出a,b,c即可;
(2)设M(x0,y0),利用A,M,P三点共线求出P点坐标,计算$\overrightarrow{BM}•\overrightarrow{BP}$得出∠MBP的范围,从而确定∠MBN的范围,进而判断出B与以MN为直径的圆的位置关系.
解答 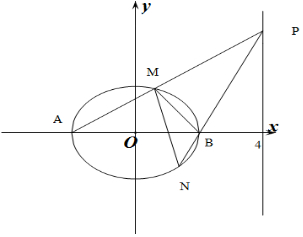 解:(1)∵长半轴的长等于焦距,△QF1F2面积的最大值为$\sqrt{3}$.
解:(1)∵长半轴的长等于焦距,△QF1F2面积的最大值为$\sqrt{3}$.
∴$\left\{\begin{array}{l}{a=2c}\\{\frac{1}{2}×2c×b=\sqrt{3}}\end{array}\right.$,又a2-b2=c2,
∴a=2,b=$\sqrt{3}$,c=1.
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)A(-2,0),B(2,0),
设M(x0,y0),则$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$,即y02=$\frac{3}{4}$(4-x02),且-2<x0<2.
∵P,A,M三点共线,∴P(4,$\frac{6{y}_{0}}{{x}_{0}+2}$),
∴$\overrightarrow{BM}$=(x0-2,y0),$\overrightarrow{BP}$=(2,$\frac{6{y}_{0}}{{x}_{0}+2}$),
∴$\overrightarrow{BM}•\overrightarrow{BP}$=2(x0-2)+$\frac{6{{y}_{0}}^{2}}{{x}_{0}+2}$=$\frac{2}{{x}_{0}+2}$(x02-4+3y02)=$\frac{2}{{x}_{0}+2}$[x02-4+$\frac{9}{4}$(4-x02)]=$\frac{5}{2}$(2-x0)>0,
∴∠MBP为锐角,
∴∠MBN为钝角,
∴点B在以MN为直径的圆内.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,7] | B. | (0,7] | C. | [$\frac{1}{3}$,7] | D. | [3,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
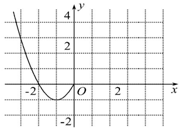 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象(二次函数图象的一部分),如图所示,请根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{i}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{i}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com