
| A. | 12 | B. | 6 | C. | 16 | D. | 8 |
分析 正实数x,y满足log2(x+3y)=log4x2+log2(2y),得:x+3y=2xy,即$\frac{1}{y}+\frac{3}{x}$=2,利用“1”的代换,即可求出3x+y的最小值.
解答 解:∵正实数x,y满足log2(x+3y)=log4x2+log2(2y),
∴(x+3y)2=x2(2y)2,整理,得:x+3y=2xy,
∴$\frac{1}{y}+\frac{3}{x}$=2,
∴3x+y=$\frac{1}{2}$(3x+y)($\frac{1}{y}+\frac{3}{x}$)=$\frac{1}{2}$(10+$\frac{3x}{y}$+$\frac{3y}{x}$)≥$\frac{1}{2}$(10+6)=8,
故选D.
点评 本题考查对数的运算,考查基本不等式的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
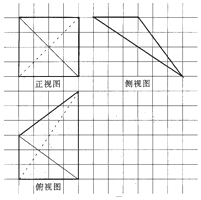 如图,网格纸上小正方形的边长为1,下图画出的是某空间几何体的三视图,则该几何体的最短棱长为( )
如图,网格纸上小正方形的边长为1,下图画出的是某空间几何体的三视图,则该几何体的最短棱长为( )| A. | 4 | B. | 5 | C. | 4$\sqrt{2}$ | D. | $\sqrt{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 流量超过1000M | 流量没有超过1000M | 合计 | |
| 男 | 20 | 25 | 45 |
| 女 | 40 | 15 | 55 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com