Question

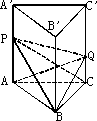
如图，已知直三棱柱ABC－的体积为V．P，Q分别是侧棱A，C上的点，且AP＝Q，求四棱锥B－APQC的体积．

Answer 1

答案：
解析：

分析：由于所求四棱锥的高及底面APQC的面积都不易求得，因此考虑将四棱锥B－APQC分割后求解． 　　解：连接PC，则将四棱锥B－APQC分割成两个三棱锥B－APC和B－PCQ， 　　因此VB－APQC＝VB－APC＋VB－PCQ． 　　连接AQ，因为S△PCQ＝S△ACQ， 　　所以三棱锥B－PCQ的体积VB－PCQ＝VB－ACQ＝VQ－ABC＝S△ABC·CQ＝S△ABC·P． 　　又VB－APC＝VP－ABC＝S△ABC·PA， 　　所以VB－APQC＝VB－APC＋VB－PCQ＝S△ABC·(PA＋P)＝V． 　　点评：如果用分割法将不规则四棱锥分割成两个三棱锥来求解是解决本题的关键的话，那么多次用到等积变换的方法，将三棱锥都转化为以△ABC为底面的等体积的三棱锥求解，更是本题解法的点睛之笔．