
分析 (I)设A(x1,y1),B(x2,y2),直线方程与抛物线方程联立化为:x2-12x+16=0,利用数量积运算性质、根与系数的关系,只要证明$\overrightarrow{OA}•\overrightarrow{OB}$=0即可得出.
(II)在x轴正半轴上存在一点P(2p,0),使得过点P任作抛物线的一条弦,并以该弦直径的圆都过原点.
下面给出分析:设经过点P的直线方程为:ty+2p=x,设直线与抛物线相交于点E(x3,y3),F(x4,y4).与抛物线方程联立化为:y2-2pty-4p2=0,利用数量积运算性质、根与系数的关系,只要证明$\overrightarrow{OE}•\overrightarrow{OF}$=0即可得出.进而得出结论.再利用中点坐标公式、根与系数的关系即可得出圆心的轨迹方程.
解答 (I)证明:设A(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}{y=x-4}\\{{y}^{2}=4x}\end{array}\right.$,
化为:x2-12x+16=0,
∴x1+x2=12,x1x2=16.
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=x1x2+(x1-4)(x2-4)=2x1x2-4(x1+x2)+16=2×16-4×12+16=0.
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$.
(II)解:先考虑一般性结论:抛物线y2=2px.
在x轴正半轴上存在一点P(2p,0),使得过点P任作抛物线的一条弦,并以该弦直径的圆都过原点.
下面给出证明:设经过点P的直线方程为:ty+2p=x,设直线与抛物线相交于点E(x3,y3),F(x4,y4).
联立$\left\{\begin{array}{l}{ty+2p=x}\\{{y}^{2}=2px}\end{array}\right.$,化为:y2-2pty-4p2=0,
△=4p2t2+16p4>0.
∴y1+y2=2pt,y1y2=-4p2.
则$\overrightarrow{OE}•\overrightarrow{OF}$=x3x4+y3y4=(ty3+2p)(ty3+2p)+y3y4=(t2+1)y3y4+2pt(y3+y4)+4p2=-4p2(t2+1)+2pt×2pt+4p2=0.
∴$\overrightarrow{OE}⊥\overrightarrow{OF}$.
∴在x轴正半轴上存在一点P(2p,0),使得过点P任作抛物线的一条弦,并以该弦直径的圆都过原点.
因此对于:抛物线y2=4x,在x轴正半轴上存在一点P(4,0),使得过点P任作抛物线的一条弦,并以该弦直径的圆都过原点.
∴m=4.
设线段EF的中点G(x0,y0).
由y1+y2=2pt=4t=2y0,解得y0=2t,
x1+x2=ty1+4+ty2+4=2ty0+8=4t2+8,∴x0=$\frac{{x}_{1}+{x}_{2}}{2}$=2t2+4,
化为:${x}_{0}=2×(\frac{{y}_{0}}{2})^{2}$+4,∴${y}_{0}^{2}$=2(x0-4).(x0≥4).
∴圆心G的轨迹方程为:${y}_{0}^{2}$=2(x0-4).(x0≥4),把x0,y0分别换成x,y,可得点G的轨迹方程为:y2=2(x-4)(x≥4).
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题、向量垂直与数量积运算性质、圆的性质,考查了推理能力与计算能力,属于难题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
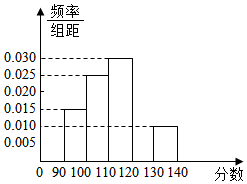 某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.
某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
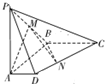 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
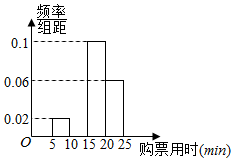 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).| 分组 | 组距 | 频数 | 频率 |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | ② |
| 四组 | 15≤t<20 | ① | 0.50 |
| 五组 | 20≤t≤25 | 30 | 0.30 |
| 合计 | 0≤t≤25 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
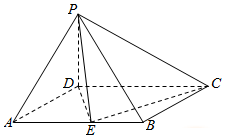 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=PD=1,AB=2,ABCD为矩形,点E是线段AB中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD=PD=1,AB=2,ABCD为矩形,点E是线段AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com