
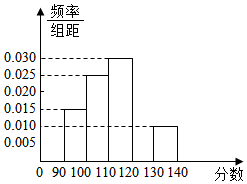
 ijУ��֯��һ��ѧģ���⣨����150�֣����ӵ÷���[90��140]��ѧ���������ȡ��100��ѧ���ijɼ��������Ƿֳ�5�飬�ֱ�Ϊ����1��[90��100������2��[100��110������3��[110��120������4��[120��130������5��[130��140]��Ȼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ��
ijУ��֯��һ��ѧģ���⣨����150�֣����ӵ÷���[90��140]��ѧ���������ȡ��100��ѧ���ijɼ��������Ƿֳ�5�飬�ֱ�Ϊ����1��[90��100������2��[100��110������3��[110��120������4��[120��130������5��[130��140]��Ȼ����Ƴ�Ƶ�ʷֲ�ֱ��ͼ������ ����������Ƶ��֮�͵���1���[120��130��Ƶ�ʣ�Ȼ���ͼ���ɣ�
����[110��120����[120��130����[130��140]�������ѧ���������ٸ��ݷֲ�����������n��
����һһ�о��������������ȡ2�˵����л����¼���ѡȡ��2��ǡΪ1��1Ů�Ļ����¼������ø��ʹ�ʽ���㼴�ɣ�
��� 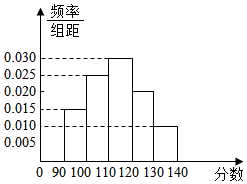 �⣺������Ƶ�ʷֲ�ֱ��ͼ��[120��130����Ƶ��Ϊ��1-��0.015+0.025+0.30+0.010����10=0.20��
�⣺������Ƶ�ʷֲ�ֱ��ͼ��[120��130����Ƶ��Ϊ��1-��0.015+0.025+0.30+0.010����10=0.20��
ֱ��ͼ��ͼ��ʾ��
����[110��120��������Ϊ0.030��10��100=30�ˣ�
[120��130��������Ϊ0.020��100=20��
[130��140]����Ϊ0.010��10��100=10�ˣ�
��$\frac{n}{30+20+10}$=$\frac{6}{20}$
��n=18��
����4��������A��B��C��D��ʾ��2��Ů����a��b��ʾ������6��ѧ������ѡ2����Ϊ�������������еĻ����¼��У�A��B������A��C������A��D������A��a������A��b������B��C������B��D������B��a����
��B��b������C��D������C��a������C��b������D��a������D��b������a��b������15����
����ȡ��2��ǡΪ1��1Ů���У�A��a������A��b������B��a������B��b������C��a������C��b������D��a������D��b����8����
��ѡȡ��2��ǡΪ1��1Ů�ĸ���Ϊ$\frac{8}{15}$��
���� ������Ҫ������Ƶ�ʷֲ�ֱ��ͼ��ƽ�������ŵ���͵ĸ������⣬���ڻ����⣮


 �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x∉P��x∉Q | B�� | x∉P��x∉Q | C�� | x��CU��P��Q�� | D�� | x��CUP |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-�ޣ�\sqrt{2}}��$ | B�� | $��{-�ޣ�2\sqrt{2}}��$ | C�� | $��{-\sqrt{2}��\sqrt{2}}��$ | D�� | $��{-2\sqrt{2}��2\sqrt{2}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com