
分析 由b>a>0,$\frac{f(b)-f(a)}{b-a}$<1恒成立,等价于f(b)-b<f(a)-a恒成立;即h(x)=f(x)-x在(0,+∞)上单调递减;h′(x)≤0,求出m的取值范围.
解答 (Ⅲ)对任意b>a>0,$\frac{f(b)-f(a)}{b-a}$<1恒成立,
等价于f(b)-b<f(a)-a恒成立;
设h(x)=f(x)-x=lnx+$\frac{m}{x}$-x(x>0),
则h(b)<h(a).
∴h(x)在(0,+∞)上单调递减;
∵h′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$-1≤0在(0,+∞)上恒成立,
∴m≥-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$(x>0),
∴m≥$\frac{1}{4}$;
对于m=$\frac{1}{4}$,h′(x)=0仅在x=$\frac{1}{2}$时成立;
∴m的取值范围是[$\frac{1}{4}$,+∞).
点评 本题考查了导数的综合应用问题,解题时应根据函数的导数判定函数的增减性以及求函数的极值和最值,应用分类讨论法,构造函数等方法来解答问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
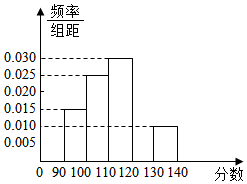 某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.
某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $2+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
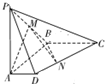 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,AD∥BC,∠ABC=90°,PA=AB=BC=2,AD=1,M是棱PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com