
分析 (1)联立方程组,消去y得关于x的一元二次方程,利用中点坐标公式以及两点间的距离公式求出半径和圆心即可得到结论.
(2)求出对应的斜率,结合根与系数之间的关系代入进行求解即可.
解答 解:(1)将直线y=$\frac{1}{2}$x+2代入$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1得x2-4x-14=0,
设A(x1,y1),B(x2,y2),
则x1+x2=4,x1x2=-14,
则AB的中点C的横坐标x=$\frac{{x}_{1}+{x}_{2}}{2}=\frac{4}{2}=2$,纵坐标y=$\frac{1}{2}×2+2=1+2=3$,即圆心C(2,3),
|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{(1+\frac{1}{4})×(16+4×14)}$=$\sqrt{\frac{5}{4}×72}$=3$\sqrt{10}$,
则半径R=$\frac{1}{2}|AB|=\frac{3\sqrt{10}}{2}$,
则圆的标准方程为(x-2)2+(y-3)2=$\frac{45}{2}$.
(2)若OA、OB所在直线的斜率分别是kOA、kOB,
则kOA=$\frac{{y}_{1}}{{x}_{1}}$,kOB=$\frac{{y}_{2}}{{x}_{2}}$,
则kOA•kOB=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{(\frac{1}{2}{x}_{1}+2)(\frac{1}{2}{x}_{2}+2)}{{x}_{1}{x}_{2}}$=$\frac{\frac{1}{4}{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}+4}{{x}_{1}{x}_{2}}$=$\frac{-14×\frac{1}{4}+4+4}{-14}$=-$\frac{9}{28}$.
点评 本题主要考查直线和双曲线位置关系的应用,利用转化法转化为一元二次方程,结合根与系数之间的关系是解决本题的关键.考查学生的运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{36}$ | B. | $\frac{1}{24}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
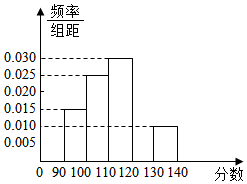 某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.
某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com