
���� ��$\sum_{\;}^{\;}$���ߵĶ����֪���߱�$\sum_{\;}^{\;}$���ߵ������Ƕ��������P1��x1��y1����T��������P2��x2��y2����T��ʹ��x1x2+y1y2=0��������OP1��OP2��Ȼ�������֤���ɵõ��𰸣�
��� �⣺��������P1��x1��y1����T������P2��x2��y2����T��ʹx1x2+y1y2=0��������OP1��OP2��
���ڢ�2x2+y2=1����2x2+y2=1��ͼ�����ԭ�����ĶԳƣ�
���������P1��x1��y1����C������P2��x2��y2����C��ʹOP1��OP2����2x2+y2=1Ϊ$\sum_{\;}^{\;}$���ߣ�
���ڢ�x2-y2=1����P1��x1��y1��Ϊ˫���ߵĶ���ʱ��˫�����ϲ����ڵ�P2��x2��y2����C��ʹOP1��OP2����x2-y2=1����$\sum_{\;}^{\;}$���ߣ�
���ڢ�y2=2x����ͼ�����y��Գƣ�OP1�Ĵ���һ�����������ཻ����y2=2xΪ$\sum_{\;}^{\;}$���ߣ�
���ڢܣ���P1��x1��y1��Ϊ��1��0��ʱ�������ϲ����ڵ�P2��x2��y2����C��ʹOP1��OP2���ʢܲ���$\sum_{\;}^{\;}$���ߣ�
���ڢݣ��ɣ�2x-y+1����|x-1|+|y-2|��=0�ɵ�2x-y+1=0��㣨1��2����
���������P1��x1��y1����C������P2��x2��y2����C��ʹOP1��OP2���ʣ�2x-y+1����|x-1|+|y-2|��=0Ϊ$\sum_{\;}^{\;}$���ߣ�
�ʴ�Ϊ���٢ۢݣ�
���� ���⿼����������ٵ��ж���Ӧ�ã�������Ԫ���뼯�ϵĹ�ϵ����������ѧת��˼�뷽�������Ĺؼ��Ƕ��¶�������⣬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
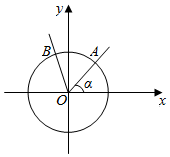 ��ͼ����Ǧ��Ķ���������ԭ�㣬ʼ����x���������غϣ��ձ��뵥λԲ���ڵ�A��x1��y1����������OA��ԭ�㰴��ʱ�뷽����ת$\frac{��}{3}$���뵥λԲ���ڵ�B��x2��y2�����Ǻ���f������=y1+y2��
��ͼ����Ǧ��Ķ���������ԭ�㣬ʼ����x���������غϣ��ձ��뵥λԲ���ڵ�A��x1��y1����������OA��ԭ�㰴��ʱ�뷽����ת$\frac{��}{3}$���뵥λԲ���ڵ�B��x2��y2�����Ǻ���f������=y1+y2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com