
| A. | $({-∞,\sqrt{2}})$ | B. | $({-∞,2\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-2\sqrt{2},2\sqrt{2}})$ |
分析 问题转化为m<$\frac{1}{2x}$+x在x∈(0,+∞)恒成立,根据基本不等式的性质求出$\frac{1}{2x}$+x在x∈(0,+∞)上的最小值,从而求出m的范围即可.
解答 解:∵f′(x)-f(x)=ex[$\frac{1}{x}$+2(x-m)]>0,
∴m<$\frac{1}{2x}$+x在x∈(0,+∞)恒成立,
而$\frac{1}{2x}$+x≥2$\sqrt{\frac{1}{2x}•x}$=$\sqrt{2}$,当且仅当x=$\frac{\sqrt{2}}{2}$时“=”成立,
故m<$\sqrt{2}$,
故选:A.
点评 本题考查了函数恒成立问题,考查导数的应用以及级别不等式的性质,是一道基础题.


 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
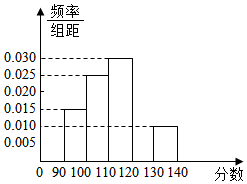 某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.
某校组织高一数学模块检测(满分150分),从得分在[90,140]的学生中随机抽取了100名学生的成绩,将它们分成5组,分别为:第1组[90,100),第2组[100,110),第3组[110,120),第4组[120,130),第5组[130,140],然后绘制成频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
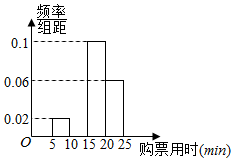 某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
某车站在春运期间为了了解旅客购票情况,随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min),下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).| 分组 | 组距 | 频数 | 频率 |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | ② |
| 四组 | 15≤t<20 | ① | 0.50 |
| 五组 | 20≤t≤25 | 30 | 0.30 |
| 合计 | 0≤t≤25 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3!}{5!}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com