练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数（），将的图象向左平移个单位长度后得到的图象，且在区间内的最大值为.

    （1）求实数的值；

    （2）在中，内角， ， 的对边分别是， ， ，若，且，求的周长的取值范围.

    【答案】（1）.（2）

    【解析】试题分析：（1）先利用两角和公式和对函数解析式化简整理，根据图象的平移确定的解析式，根据的范围和三角函数的图象与性质确定的最大值的解析式，求得；（2）根据第一问中函数的解析式确定的值，进而利用余弦定理和基本不等式确定的范围，最后确定周长的范围.

    试题解析：（1）由题设得 .

    所以 .

    因为当时， .

    令，即时， ，所以.

    （2）由已知得.因为在中， ，所以，

    所以，所以，即.

    又因为，由余弦定理，得

    ，当且仅当时等号成立.又因为，所以，所以的周长

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x3-3ax+e，g（x）=1-lnx，其中e为自然对数的底数.

    （I）若曲线y=f（x）在点（1，f（1））处的切线与直线l：x+2y=0垂直，求实数a的值；

    （II）设函数F（x）=-x[g（x）+x-2]，若F（x）在区间（m,m+1）（m∈Z）内存在唯一的极值点，求m的值；

    （III）用max{m，n}表示m，n中的较大者，记函数h（x）=max{f（x），g（x）}（x>0）. 若函数h（x）在（0，+∞）上恰有2个零点，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面几种推理是合情推理的是

    ①由圆的性质类比出球的有关性质;②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°;③教室内有一把椅子坏了，则该教室内的所有椅子都坏了;④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得出凸多边形的内角和是(n－2)·180°___________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在处取得极值．

    （1）求函数的解析式；

    （2）设函数，若对任意的，总存在唯一的（为自然对数的底数）使得，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）求函数在上的最小值；

    （2）对一切，恒成立，求实数的取值范围；

    （3）探讨函数是否存在零点？若存在，求出函数的零点；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四个结论：

    （1）如果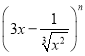的展开式中各项系数之和为128，则展开式中的系数是-21；

    （2）用相关指数来刻画回归效果， 的值越大，说明模型的拟合效果越差；

    （3）若是上的奇函数，且满足，则的图象关于对称；

    （4）一个篮球运动员投篮一次得3分的概率为，得2分的概率为，不得分的概率为，且，已知他投篮一次得分的数学期望为2，则的最小值为；

    其中正确结论的序号为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形，侧棱底面， ， 是的中点.

    （1）求二面角的平面角的余弦值；

    （2）在被上是否存在点，使平面？证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在△ABC中，角A，B，C所对的边分别为a，b，c，且2S△ABC＝·.

    (1)求角B的大小；

    (2)若b＝2，求a＋c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x2＋bx为偶函数，数列{an}满足an＋1＝2f(an－1)＋1，且a1＝3，an>1.

    (1)设bn＝log2(an－1)，证明：数列{bn＋1}为等比数列；

    (2)设cn＝nbn，求数列{cn}的前n项和Sn.

    查看答案和解析>>

    同步练习册答案