
分析 (1)求导数得到f′(x)=3(x-1)(x-3),根据导数符号便可判断f(x)的单调性,并判断f(x)过原点,f(1)=4,f(3)=0,这样便可画出f(x)的草图;
(2)可设g(x)=x3-6x2+9x+a,从而g(x)是由f(x)向上或向下平移|a|个单位得到,这样根据题意即可得出g(x)有两个零点,根据上面画出的草图便可观察出a的取值,从而得出a的取值范围.
解答 解:(1)f′(x)=3x2-12x+9=3(x-1)(x-3);
∴x<1,或x>3时,f′(x)>0,1<x<3时,f′(x)<0;
即f(x)在(-∞,1),(3,+∞)上单调递增,在(1,3)上单调递减,且f(0)=0,f(1)=4,f(3)=0;
∴f(x)的草图如下: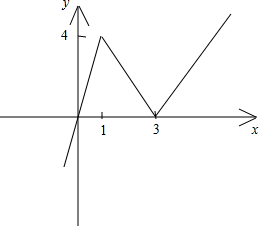
(2)设g(x)=x3-6x2+9x+a,则g(x)是f(x)沿y轴向上或向下平移|a|个单位得到;
∵方程x3-6x2+9x+a=0有2个实根;
∴g(x)有两个零点;
根据上面的草图得,a=0,或a=-4;
∴a的取值范围为{-4,0}.
点评 考查基本初等函数的求导,根据导数符号判断函数单调性的方法,根据函数单调性及极值点的坐标画函数草图的方法,函数图象沿y轴方向上的平移变换,以及函数零点的定义,数形结合解题的方法.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 22 | C. | 18 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $-\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{{3\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该函数的值域是[-1,1] | |
| B. | 当且仅当2kπ+π<x<2kπ+$\frac{3π}{2}$(k∈Z)时,f(x)<0 | |
| C. | 当且仅当x=2kπ+$\frac{π}{2}$(k∈Z)时,该函数取得最大值 | |
| D. | 该函数是以π为最小正周期的周期函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com