
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由已知可得$\left\{\begin{array}{l}{sin2θ<0}\\{cosθ<0}\end{array}\right.$,则$\left\{\begin{array}{l}{sinθ>0}\\{cosθ<0}\end{array}\right.$,分别求得θ的范围,再取交集得答案.
解答 解:∵点P(sin2θ,cosθ)在第三象限,
∴$\left\{\begin{array}{l}{sin2θ<0}\\{cosθ<0}\end{array}\right.$,则$\left\{\begin{array}{l}{sinθ>0}\\{cosθ<0}\end{array}\right.$,
由sinθ>0,知θ为第一、第二或y轴正半轴上的角;
由cosθ<0,知θ为第二、第三或x轴负半轴上的角.
∴θ为第二象限角.
故选:B.
点评 本题考查三角函数的象限符号,考查交集运算思想方法,是基础题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
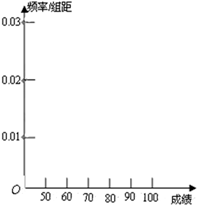 某校高二年级的600名学生参加一次科普知识竞赛,然后随机抽取50名学生的成绩进行统计分析.
某校高二年级的600名学生参加一次科普知识竞赛,然后随机抽取50名学生的成绩进行统计分析.| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.1 |
| [60,70) | 10 | 0.2 |
| [70,80) | 15 | 0.3 |
| [80,90) | 15 | 0.3 |
| [90,100) | 5 | 0.1 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}+\sqrt{10}>\sqrt{3}+\sqrt{14}$ | B. | $\sqrt{7}+\sqrt{10}<\sqrt{3}+\sqrt{14}$ | C. | $\sqrt{7}+\sqrt{10}=\sqrt{3}+\sqrt{14}$ | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com